一、二次函数的定义
函数$y=ax^2+bx+c(a \neq 0)$叫做二次函数，$x$是自变量，定义域是$R$。
二、二次函数的表示形式
⑴一般式：$y=ax^2+bx+c(a \neq 0)$；
⑵顶点式：$y=a\left(x+\dfrac{b}{2a}\right)^2+\dfrac{4ac-b^2}{4a}$，顶点坐标$\left(-\dfrac{b}{2a},\dfrac{4ac-b^2}{4a}\right)$；
⑶零点式：$y=a(x-x_1)(x-x_2)$，其中$\Delta =b^2-4ac$，$x_1,x_2$是抛物线与x轴交点的横坐标，
这时两交点的距离为$|x_1-x_2|=\sqrt{(x_1+x_2)^2-4x_1 x_2}=\dfrac{\sqrt{b^2-4ac}}{|a|}=\dfrac{\sqrt{\Delta}}{|a|}$。

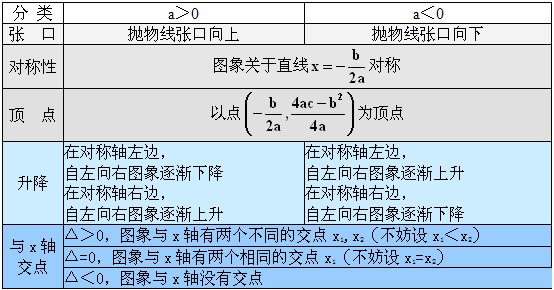
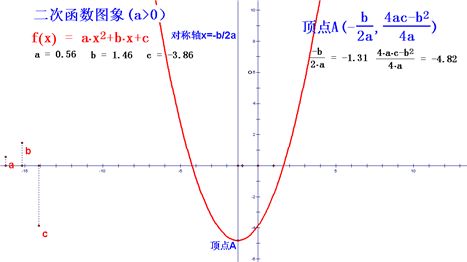
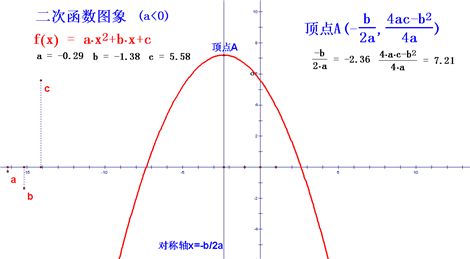
三、二次函数的图象
二次函数图象是以直线$x=-\dfrac{b}{2a}$为对称轴，以点$\left(-\dfrac{b}{2a},\dfrac{4ac-b^2}{4a}\right)$为顶点的抛物线。
图象特征：