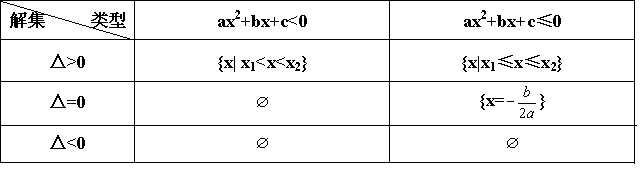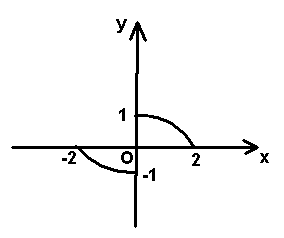二、重点难点
    重点:理解并熟练掌握解简单的高次整式不等式、分式不等式和含绝对值不等式.

    难点:含字母类高次整式不等式、分式不等式的解法．

    三、特别提示
    (1)解不等式的基础是一元一次不等式(组)、一元二次不等式(组)，而解不等式的关键是同解变形，变形规律是：无理`rarr`有理：分式`rarr`整式；高次`rarr`低次；二次`rarr`一次 ．在此过程中，要注意逻辑联结词“或”“且”的运用，以及解集的“交”“并”的运算，在较复杂情况下，可画数轴求“交”“并”集，以免出错．
　　(2)解一元二次不等式时，若二次项系数含有字母，应对二次项系数的符号进行分类讨论，若二次项系数为负，可两边同乘以-1，转化为正的，但此时不等号要改变方向 ．若相应二次方程根的大小不确定，应先讨论根的大小，再写出解集．
　　(3)解分式不等式时，不要直接去分母(当分母符号不确定时)，要移项，化右边为零．若是解含等号的分式不等式，要注意分母的根不能写在解集里．
　　(4)在解含参数的不等式时，往往要分类讨论，分类时要标准明确，不重不漏．
　　(5)用穿根法来解分式不等式、高次不等式比较方便，但在穿根时要注意把不等式整理成标准形式，即各因式中未知数x的系数为1．
　　(6)解各种类型的不等式都有其“通法”，也有“巧法”，切不可偏爱“巧法”而忽视“通法”，否则将是本末倒置．

    1、一元一次不等式的解法
    一元一次不等式`ax>b`的解集为
    ①当`a>0`时，解集为`x>b/a`
    ②当`a<0`时，解集为`x<b/a`
    ③当`a=0`时，若`b>=0`，则为`x=O/`；若`b<0`，则为`x in RR`
    2、一元二次不等式的解法
    设`a>0，x_1，x_2`是方程`ax^2+bx+c=0`的两实根，且`x_1<x_2`，一元二次不等式的解集如下表所示：   

       
    3、分式不等式的解法
    先将不等式整理为`f(x)/g(x)>0`或`f(x)/g(x)>=0`的形式，再转化为整式不等式求解，即：
    `f(x)/g(x)>0 hArr f(x)g(x)>0`
    `f(x)/g(x)>=0 hArr {(f(x)g(x)>=0),(g(x)!=0):}`
    4、简单的一元高次不等式的解法
    一元高次不等式`f(x)>0`，用数轴标根法(或称区间法、穿根法)求解，其步骤是：
    (1)将`f(x)`的最高次项的系数化为正数；
    (2)将`f(x)`分解为若干个一次因式的积或二次不可分因式之积；
    (3)将每一个一次因式的根标在数轴上，从右上方依次通过每一点画曲线；
    (4)根据曲线显现出`f(x)`的值的符号变化规律，写出不等式的解集；
    (5)奇次根依次穿过，偶次根穿而不过．
    5、指数、对数不等式的解法
    (1)`a^f(x)>a^g(x) hArr {(f(x)<g(x),   0<a<1),(f(x)>g(x),   a>1):}`；
    (2)`log_a f(x)>log_a g(x) hArr {(f(x)<g(x),   0<a<1),(f(x)>g(x),   a>1):}`

    应用举例
    一、应用特点
    1、含参数的不等式的解法
    2、一元二次方程、一元二次函数和一元二次不等式之间的相交点位置与不等式的互相转化
    3、正确利用函数的图象和性质解不等式

    二、案例示范
    (回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

    1、解关于`x`的不等式`(x-a)/(x-a^2)<0(a in RR)`

提示	示范
要使分式小于零，必须分子、分母异号，于是原不等式等价于两个一次不等式组的并集，再将a划分为几个合适的区间求解．
解:原不等式等价于`(x-a)(x-a^2)<0`     `:.`当`a>a^2`，即`0<a<1`时，`a^2<x<a`；     当`a<a^2`，即`a>1`或`a<0`时，`a<x<a^2`；     当`a=a^2`，即`a=0`或`a=1`时，`x in O/`．     `:.`当` 0<a<1`时，解集为`(a^2，a)`；     当`a>1`或`a<0`时， 解集为`(a，a^2)`；     当`a=0`或`a=1`时，解集为`O/`．     评注:含参数不等式的解是条件解，必须标明参数的相应取值范围，且解集不能并；讨论参数时不要重复，也不要遗漏，特别是不要遗漏两根相等的情况．

提示	示范
用数形结合的思想，将其转化为不等式组．
解:方程`2kx^2-2x-3k-2=0`的两个实根一个小于1，另一个大于1，也就是对应的二次函数图象与`x`轴交于点`(1，0)`的两侧．     设`f(x)=2kx^2-2x-3k-2=0`，则`{(k>0),(f(1)<0):}或{(k<0),(f(1)>0):}`即`kf(1)<0`，     即`k(k+4)>0`     `:.k<-4`或`k>0`     评注:`f(x)=ax^2+bx+c(a!=0)`的图象与`x`轴的交点位于点`(x_0，0)`两侧的充要条件是`af(x_0)<0`

(1)求`f(4)`的值；

(2)当`a>0`时，解关于`x`的不等式`f(1/x)+f(x^2+a)<=2`

提示	示范
根据题目条件，列出不等式组，再进行分类讨论．
解:(1)令`x=y=2`，代入`f(xy)=f(x)+f(y)`得`f(4)=2f(2)`     `.:f(2)=1`     `:.f(4)=2`     (2)由已知及(1)得`f((x^2+a)/x)<=f(4) rArr {(1/x>0),(x^2+a>0),((x^2+a)/x<=4):}，     解此不等式组，得     当`a>4`时，解集为`O/`；     当`0<a<=4`时，解集为`[2-sqrt(4-a)，2+sqrt(4-a)]`     评注:本题是一道与函数有关的问题，由于未给出函数解析式，故对此类题目一定要充分运用函数的性质，如单调性、奇偶性等．

    实践体验
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高.)

    1、如图，函数`y=f(x)`的图象是中心在原点，焦点在`x`轴上的椭圆的两段弧，则不等式`f(x)<f(-x)+x`的解集为(   ) 

     
    A．`(-sqrt(2)，0) uu (sqrt(2)，2]` 　　　      B．`[-2，- sqrt(2)) uu (sqrt(2)，2]`

    C．`[-2，0)uu(0， sqrt(2)]`　　　　　　　 D．`[-2，- sqrt(2)/2) uu (sqrt(2)/2，2]`

提示	示范
由题中所给条件可知，这是个椭圆的局部图形，由此可得椭圆的方程，从而进行不等式求解。
解:由题意知椭圆方程为`x^2/4+y^2=1`．当`x>0，y>0`时，`y=f(x)=sqrt(1-x^2/4)`．     又知`f(x)`为奇函数，故`f(x)<f(-x)+x`可化为`f(x)<x/2`．     令`g(x)=x/2`，当`x>0`时，`f(x)=g(x)`，即`sqrt(1-x^2/4)=x/2`，解得`x=sqrt(2)`．     由图象易知`sqrt(2)<x<=2`时，`f(x)<g(x)`．     又`f(x)`为奇函数，故`-sqrt(2)<x<0`时，`f(x)<g(x)`也成立．     答案：A     评注:解不等式除去利用基本的不等式的解法之外，还可以利用函数的单调性、数形结合等方法来求解．利用数形结合解不等式时，一要从不等式的两边得到两函数`y=f(x)，y=g(x)`；二是两函数的图象容易作出；三是图象的相对位置及交点坐标要力求准确．

    2、已知函数`f(x)`和`g(x)`的图象关于原点对称，且`f(x)=x^2+2x`．
    (1)求函数`g(x)`的解析式；
    (2)解不等式`g(x)>=f(x)-|x-1|`；
    (3)若`h(x)=g(x)-lambda f(x)+1`在[-1，1]上是增函数，求实数`lambda`的取值范围．

提示	示范
(提示内容)
解:(1)设函数`y=f(x)`的图象上任一点`Q(x_0，y_0)`关于原点的对称点为`P(x，y)`，则`{((x_0+x)/2=0),(( y_0+y)/2=0):}`，即`{(x_0=-x),(y_0=-y):}`     `:.`点`Q(x_0，y_0)`在函数`y=f(x)`的图象上．     `:.-y=x^2-2x`，即`y=-x^2+2x`     故`g(x)=-x^2+2x`． 　　(2)由`g(x)>=f(x)-|x-1|`，可得`2x^2-|x-1|<=0`     当`x>=1`时，`2x^2-x+1<=0`，此时不等式无解．     当`x<1`时，`2x^2-x+1<=0，     `:.-1<=x<=1/2`．     因此，原不等式的解集为`[-1，1/2]` 　　(3)`h(x)=-(1+lambda)x^2+2(1-lambda)x+1`     ①当`lambda=-1`时，     `h(x)=4x+1`在`[-1，1]`上是增函数，     `:.lambda=-1`．     ②当`lambda!=-1`时，对称轴的方程为`x=(1-lambda)/(1+lambda)`．     当`lambda<-1`时，`(1-lambda)/(1+lambda)<=-1`，解得`lambda<-1`．     当`lambda>-1`时，`(1-lambda)/(1+lambda)>=1`，解得`-1<lambda<=0`．     综上，`lambda<=0`     评注:不等式与函数综合题，其题型主要有两类：一类是不等式作为工具在函数中加以应用，如求函数的定义域、值域等；另一类就是利用函数的性质解不等式．

    学习感悟
    1、含有参数的不等式的解法．
    解含有参数的不等式问题，一般分为两大类，一类是已知参数范围，求不等式的解；另一类是求满足不等 式的解的参数的取值范围．
    解答含参数的不等式时，一般都要对参数进行分类讨论，但对分类标准的把握要做到准确．当参数在不等式某些特殊位置时，其分类标准有一定的规律:
    (1)一元一次不等式的一次项系数含有关于参数a的代数式`f(a)`时，需对`f(a)`分`f(a)>0`，`f(a)=0`，`f(a)<0`三种情况讨论．
    (2)一元二次不等式中，若二次项系数是含有关于参数`a`的代数式`f(a)`，就需对`f(a)`分为`f(a)=0`和`f(a)!=0`两种情况讨论．而当`f(a)!=0`时，又要对判别式`Delta`需分：
    `Delta>0`，`Delta=0`，`Delta<0`三种情况讨论．
    (3)若对数或指数中的底数中含有参数`m`，则需对`a`分`a>1`和 `0<a<1`两种情况讨论．
    分类讨论的关键在于掌握分类标准，分类要做到不重不漏．对于有两个(或两个以上)参数根据题目的需要先对其中一个参数分类讨论，在此基础上，如果还需要对另一个参数进行讨论，则要进行下一级讨论．讨论要逐级进行，不能越级．特别注意讨论出现混乱现象．
    2、解含绝对值的不等式的主要思路是去掉绝对值符号，常用方法有三种：
    (1)讨论：或利用绝对值的概念或利用`“a>0`时，`|x|<a hArr –a<x<a；|x|>a hArr x<-a`或`x>a`”去掉绝对值符号求解；
    (2)两边平方；
    (3)数形结合法
    3、数形结合法是解绝对值不等式的一种重要方法，因此要熟练掌握函数`|f(x)|`和`f(|x|)`的图象的画法．
    4、含有绝对值的不等式的证明一般有两种方法：一是利用三角不等式`||a|-|b||<=|a+-b|<=|a|+|b|`进行合理的放缩；二是转化为分段函数，利用函数的思维方法求解．
    5、在应用定理：`||a|-|b||<=|a+-b|<=|a|+|b|`证明含绝对值的不等式或求含绝对值函数的最值时，一定要注意等号成立的条件．