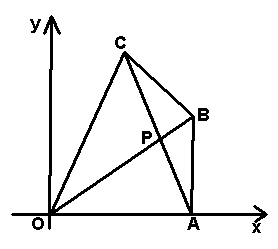一、复习目标
    理解平面向量的坐标的概念，掌握平面向量的坐标运算.   

    二、重点难点
    (这里输入)

    三、特别提示
    (1)向量的坐标等于表示该向量的有向线段的终点坐标减去起点坐标，只有当向量的起点在原点时，向量的坐标才与其终点坐标相同，向量是可以自由平移的，其坐标在移动前后不变.
    (2)两向量共线的充要条件的坐标表示是`x_1 y_2 - x_2 y_1=0`，在应用时要特别注意，不能混淆.
    (3)向量的坐标表示实际上就是向量的代数表示，向量的坐标运算使向量的运算完全代数化，这正是数形结合思想方法的重要体现，由于坐标运算方便，可操作性强，因此在求解有关问题时，可尽量采用向量的坐标运算.

    知识梳理

    1、平面向量的坐标表示
   在平面直角坐标系内，分别取与`x`轴、`y`轴正方向相同的两个单位向量`vec(i)`、`vec(j)`作为基底，对任一向量`vec(a)`，有且只有一对实数`x`、`y`，使得`vec(a)=xvec(i)+yvec(j)`，则实数对`(x，y)`叫做向量`vec(a)`的直角坐标，记作`vec(a)=(x，y)`，其中`x`、`y`分别叫做`vec(a)`在`x`轴、`y`轴上的坐标，`vec(a)=(x，y)`叫做向量`vec(a)`的坐标表示.
    相等的向量其坐标相同，坐标相同的向量是相等向量.
    2、平面向量的坐标运算
    (1)已知点`A(x_1，y_1)`，`B(x_2，y_2)`，则`vec(AB)=(x_2-x_1，y_2-y_1)`，`|vec(AB)|=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
    (2)已知`vec(a)=(x_1，y_1)`，`vec(b)=(x_2，y_2)`，则
     `vec(a)+vec(b)=(x_1+x_2，y_1+y_2)`，
     `vec(a)-vec(b)=(x_1-x_2，y_1-y_2)`，
     `lambda vec(a)=(lambda x_1，lambda y_1)`，
     `vec(a)"//"vec(b)(vec(b)!=vec(0))`的充要条件是`x_1 y_2 - x_2 y_1=0`.
    (3)非零向量`vec(a)=(x，y)`的单位向量为______或______.

    应用举例
    一、应用特点
    1、向量的坐标运算
    2、向量的平行问题
    3、求点的轨迹

    二、案例示范
    (回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

    1、已知向量`vec(u)=(x，y)与向量vec(v)=(y，2y-x)`的对应关系用`v=f(u)`表示.
    (1)若`vec(a)=(1，1)，vec(b)=(1，0)`，试求向量`f(vec(a))及f(vec(b))`的坐标；
    (2)求使`f(vec(c))=(4，5)`的向量`vec(c)`的坐标；
    (3)对于任意的向量`vec(a)、vec(b)`及常数`m、n`，证明：`f(ma+nb)=mf(vec(a))+nf(vec(b))`.

提示	示范
运用向量坐标运算法则进行求解.
解:(1)由题 意，若`vec(u)=(x，y)`，则`vec(v)=(y，2y-x)=f(vec(u))`.     若`vec(a)=(1，1)，vec(b)=(1，0)`，则`f(a)=(0，2 xx 1-1)=(1，1)，f(vec(b))=(0，2 xx 0-1)=(0，-1)`     (2)设`vec(c)=(x，y)`，则`f(vec(c))=(y，2y-x)=(4，5)`     `:.{(y=4),(text{2y-x=5}):}`得`{(x=3),(text{y=4}):}`     `:.vec(c)=(3，4)`     (3)证明：设`vec(a)=(a_1，a_2)，vec(b)=(b_1，b_2)`，则`mvec(a)+nvec(b)=(ma_1+nb_1，ma_2+nb_2)`，     `f(mvec(a)+nvec(b))=(ma_2+nb_2，2ma_2+2nb_2-ma_1-nb_1)`，     又`mf(vec(a))+nf(vec(b))=m(a_2，2a_2-a_1)+n(b_2，2b_2-b_1)=(ma_2+nb_2，2ma_2+2nb_2-ma_1-nb_1)`，     `:.f(mvec(a)+nvec(b))=mf(vec(a))+nf(vec(b))`     评注:本题综合了向量的坐标运算与函数关系.

提示	示范
本题考查向量的运算.
解:由题可知：`vec(AB)=lambda vec(a)=(2lambda，3lambda)`，并有`lambda>0`.     又`|vec(AB)|=2sqrt(13) rArr sqrt((2lambda)^2+(3lambda)^2)=2sqrt(13) rArr lambda^2=4 rArr lambda=2`.     则`vec(AB)=(4，6)`，`vec(OB)=vec(OA)+vec(AB)=(1，-2)+(4，6)=(5，4)`，即点`B`的坐标为`(5，4)`.     评注:注意向量同向概念的理解与应用.

    3、已知抛物线`y^2=4x`，顶点为`O`，动直线`l:y=k(x+1)`与抛物线交于`A`，`B`两点，求满足`vec(OM)=vec(OA)+vec(OB)`的点`M`的轨迹方程.

提示	示范
将直线与曲线方程联立，并表示出`vec(OA)+vec(OB)`(本质即`(x_1+x_2，y_1+y_2)`)消去参数`k`即可.
解:设`M(x，y)`，`A(y_1^2/4，y_1)`，`B(y_2^2/4，y_2)`     则由`vec(OM)=vec(OA)+vec(OB)`得`(x，y)=(y_1^2/4，y_1)+(y_2^2/4，y_2)=((y_1^2+y_2^2)/4，y_1+y_2)`     `:.x=(y_1^2+y_2^2)/4=((y_1+y_2)^2-2y_1y_2)/4`，`y=y_1+y_2`     联立方程组`{(y^2=4x),(text{y=k(x+1)}):}`消去`x`得，`ky^2-4y+4k=0`     则`y_1`，`y_2`是方程的两根，且`y_1y_2=4`     `:.x=(y_1+y_2)^2/4-2`，     `:.x=y^2/4-2`，即`y^2=4x+8`     又`.:x=(y_1^2+y_2^2)/4>(2y_1y_2)/4=2`，     `:.`点`M`的轨迹方程为`y^2=4x+8(x>2)`     评注:本题用向量的坐标运算解决解析几何问题，这是向量应用的一个重要体现.2004、2005年均将向量与解析几何综合，而2002年天津卷将平面向量与等差数列、解析几何中的轨迹方程等融于一题，应视为一重要的考查方式.

    实践体验
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高)

    1、如图所示，已知`A(4，0)`，`B(4，4)`，`C(2，6)`，求`AC`和`OB`的交点`P`的坐标.

   

提示	示范
已知四边形四顶点的坐标求其对角线交点的坐标，一般可利用共线向量的充要条件求解.
解:方法一：设点`P`的坐标为`(x，y)`，则`vec(OP)=(x，y)`，`vec(OB)=(4，4)`     `.:vec(OP)`、`vec(OB)`共线，     `:.4x-4y=0` ①     又`.:vec(CP)=(x-2，y-6)`，`vec(CA)=(2，-6)`且向量`vec(CP)`、`vec(CA)`共线     `:.-6(x-2)-2(y-6)=0` ②     解①②得`x=3`，`y=3`，     `:.`点`P`的坐标为`(3，3)`     方法二：`.: vec(OP)"//"vec(OB)`，     `:.`设`vec(OP)=lambda vec(OB)=(4lambda，4lambda)`，     `:.vec(AP)=vec(OP)-vec(OA)=(4lambda，4lambda)-(4，0)=(4lambda-4，4lambda)`     又`vec(AC)=(2，6)-(4，0)=(-2，6)`，且`vec(AC)"//"vec(AP)`，     `:.(4lambda-4) xx 6-4lambda xx (-2)=0`     解之，得`lambda=3/4`.     `:.vec(OP)=(3，3)`.     故`P`点坐标为`(3，3)`.     评注:向量的坐标表示实际上是向量的代数表示.向量的坐标和点的坐标都是有序实数对，但向量的坐标可以进行加法、减法、数乘运算，而点的坐标是不能运算的，当起点在原点时，向量的坐标与其终点坐标是相同的，因此，求点P的坐标可以转化为求`vec(OP)`的坐标.已知四边形四顶点的坐标求其对角线交点的坐标，一般可利用共线向量的充要条件求解，这就要充分利用已知几何图形的性质，如三点共线、线段互相平行等，以便找出共线的向量，建立方程或方程组，求出结果.

    2、在直角坐标系`xOy`中，已知点`A(0，1)`和点`B(-3，4`).若点`C`在`/_AOB`的平分线上且`vec(OC)=2`，则`vec(OC)=`______

提示	示范
注意向量的运算同内角平分线定理的结合.
解:`vec(AB)=vec(OB)-vec(OA)=(-3，4)-(0，1)=(-3，3)`     设`/_AOB`的平分线交`AB`于`D`点，由内角平分线定理，知`vec(AD)=1/6vec(AB)=(-1/2，1/2)`     `:.vec(OD)=vec(OA)+vec(AD)=(-1/2，3/2)，|vec(OC)|/|vec(OD)|=2/(sqrt(10)/2)=4/(sqrt(10))=(2sqrt(10))/5`     `:.vec(OC)= (2sqrt(10))/5 vec(OD)=(-sqrt(10)/5， (3sqrt(10))/5)`     答案：`(-sqrt(10)/5， (3sqrt(10))/5)`     评注:本题考查向量的运算同内角平分线定理的结合；另外此题也可利用向量的加法运算，`vec(OC)=lambda(vec(OA)/|vec(OA)|+vec(OB)/|vec(OB)|)`来计算`vec(OC)`.

    学习感悟
    1、建立平面向量的坐标，基础是平面向量基本定理．因此，对所给向量应会根据条件在`x`轴和`y`轴进行分解，求出其坐标.向量的坐标表示，实际是向量的代数表示.在引入向量的坐标表示后，即可使向量运算完全代数化，将数与形紧密地结合了起来.这样，很多几何问题就转化为学生熟知的数量的运算.
    2、已知向量的始点和终点坐标求向量的坐标时一定要搞清方向，用对应的终点坐标减始点坐标．本节易忽略点：一是易将向量的终点坐标误为向量的坐标；二是向量共线的坐标表示易与后面向量垂直的坐标表示混淆.