2004年
解答题
(17)(本小题满分12分)
解方程![]()
18.(本小题满分12分)已知![]() 为锐角,且
为锐角,且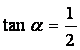 ,求
,求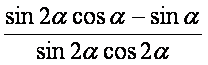 的值.
的值.
(19) (本上题满分12分)
设数列![]() 是公差不为零的等差数列,Sn是数列
是公差不为零的等差数列,Sn是数列![]() 的前n项和,且
的前n项和,且![]()
![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
20.(本小题满分12分)某村计划建造一个室内面积为800![]() 的矩形蔬菜温室。
的矩形蔬菜温室。
在温室内,沿左.右两侧与后侧内墙各保留1![]() 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3![]() 宽
宽
的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
21.(本小题满分12分)三棱锥P-ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3,
(1)求证:AB ⊥ BC;
(2)设AB=BC=![]() ,求AC与平面PBC所成角的大小.
,求AC与平面PBC所成角的大小.
22.(本小题满分12分)设椭圆 的两个焦点是
的两个焦点是![]() 与
与![]() ,
,
且椭圆上存在一点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() 是相应于焦点
是相应于焦点![]() 的准线,直线
的准线,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若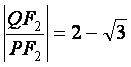 ,
,
求直线![]() 的方程.
的方程.
2005年
解答题
(17)(本小题满分12分)
已知函数![]() 求使
求使![]() 为正值的
为正值的![]() 的集合
的集合![]()
(18)(本小题满分12分)
设甲、乙、丙三台机器是否需要照顾相互之间没有影响![]() 已知在某一小时内,甲、
已知在某一小时内,甲、
乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照
顾的概率为0.125,
(Ⅰ)求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少;
(Ⅱ)计算这个小时内至少有一台需要照顾的概率![]()
19.(本小题满分12分)
四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,
平面VAD⊥底面ABCD![]()
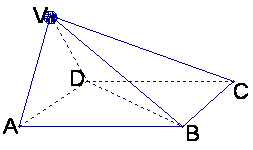 1)求证AB⊥面VAD;
1)求证AB⊥面VAD;
2)求面VAD与面VDB所成的二面角的大小.
(20)(本小题满分12分)
在等差数列![]() 中,公差
中,公差![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项,已知数列
的等差中项,已知数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,
……,![]() ,……成等比数列,求数列
,……成等比数列,求数列![]() 的通项
的通项![]()
![]()
(21) (本小题满分12分)
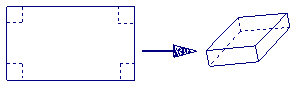 用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去
一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为
多少时,容器的容积最大?最大容积是多少?
(22) (本小题满分14分)
设![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是AB的垂直平分线,
是AB的垂直平分线,
(Ⅰ)当且仅当![]() 取何值时,直线
取何值时,直线![]() 经过抛物线的焦点F?证明你的结论;
经过抛物线的焦点F?证明你的结论;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程
的方程![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。