2004年

解答题

17．（本小题满分12分）

已知锐角三角形ABC中，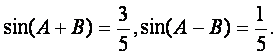

   （Ⅰ）求证：；

   （Ⅱ）设AB=3，求AB边上的高.

解答

18．（本小题满分12分）

       已知8支球队中有3支弱队，以抽签方式将这8支球队分为A、B两组，每组4支.

求：（Ⅰ）A、B两组中有一组恰有两支弱队的概率；

    （Ⅱ）A组中至少有两支弱队的概率.

解答

19．（本小题满分12分）

数列的前n项和记为S_n，已知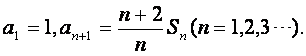证明：

（Ⅰ）数列是等比数列；

（Ⅱ）

 解答

20．（本小题满分12分）

   如图，直三棱柱ABC—A₁B₁C₁中，∠ACB=90°，AC=1，CB=，

侧棱AA₁=1，侧面AA₁B₁B的两条对角线交点为D，B₁C₁的中点为M.

（Ⅰ）求证CD⊥平面BDM；

（Ⅱ）求面B₁BD与面CBD所成二面角的大小.

       解答

21．（本小题满分12分）

给定抛物线C：y²=4x，F是C的焦点，过点F的直线l与C相交于A、B两点。

（Ⅰ）设l的斜率为1，求与的夹角的大小；

（Ⅱ）设，若λ∈[4,9]，求l在y轴上截距的变化范围.

解答

22．（本小题满分14分）

已知函数f(x)=ln(1+x)－x，g(x)=xlnx.

（Ⅰ）求函数f(x)的最大值；

（Ⅱ）设0<a<b,证明0<g(a)+g(b)-2g()<(b-a)ln2.

解答

2005年

解答题

（17）（本小题满分12分）

设函数，求使的取值范围．

解答

（18） （本小题满分12分）

已知是各项均为正数的等差数列，、、成等差数列．又，…

（Ⅰ）证明为等比数列；

（Ⅱ）如果无穷等比数列各项的和，求数列的首项和公差．

（注：无穷数列各项的和即当时数列前项和的极限）

解答

（19）（本小题满分12分）

甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.6，

本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没

有影响．令为本场比赛的局数．求的概率分布和数学期望．（精确到0.0001）

解答

（20）（本小题满分12分）

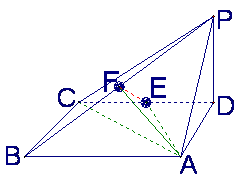     如图，四棱锥P-ABCD中，底面ABCD为矩形，PD垂直于底面ABCD，AD=PD，E、F分别

     为CD、PB的中点．

    （Ⅰ）求证：EF垂直于平面PAB；

    （Ⅱ）设AB=BC，求AC与平面AEF所成的角的大小．

解答

（21）（本小题满分14分）

P、Q、M、N四点都在椭圆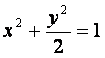上，F为椭圆在y轴正半轴上的焦点．已知

与共线，与共线，且．求四边形PMQN的面积的最小值和最大值．

解答

（22）（本小题满分12分）

已知，函数．

（Ⅰ）当x为何值时，f(x)取得最小值？证明你的结论；

（Ⅱ）设f(x)在[-1,1]上是单调函数，求a的取值范围．

解答

2006

解答题

（17）（本小题满分１２分）

              已知向量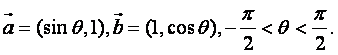

       （I）若求

       （II）求的最大值。

  解答

（18）（本小题满分１２分）

某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，

再从每箱中任意抽取2件产品进行检验。设取出的第一、二、三箱中

分别有0件、1件、2件二等品，其余为一等品。

（I）用表示抽检的6件产品中二等品的件数，求的分布列及的数学期望；

（II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，

求这批产品被用户拒绝购买的概率。

解答

（19）（本小题满分１２分）

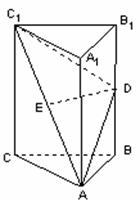
  如图，在直三棱柱中，、分别为、的中点。

       （I）证明：ED为异面直线与的公垂线；

       （II）设求二面角的大小。

         解答

（20）（本小题满分１２分）

 设函数若对所有的都有成立，

求实数的取值范围。

解答

（21）（本小题满分为１４分）

已知抛物线的焦点为F，A、B是热线上的两动点，且

过A、B两点分别作抛物线的切线，设其交点为M。

       （I）证明为定值；

       （II）设的面积为S，写出的表达式，并求S的最小值。

解答

（22）（本小题满分１２分）

              设数列的前项和为，且方程

              有一根为

       （I）求

       （II）求的通项公式

 解答

2007年

解答题

17．（本小题满分10分）

在中，已知内角，边．设内角，周长为．

（1）求函数的解析式和定义域；

（2）求的最大值．

解答

18．（本小题满分12分）

从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件：

“取出的2件产品中至多有1件是二等品”的概率．

（1）求从该批产品中任取1件是二等品的概率；

（2）若该批产品共100件，从中任意抽取2件，表示取出的2件产品中

二等品的件数，求的分布列．

解答

19．（本小题满分12分）

如图，在四棱锥中，底面为正方形，

侧棱底面分别为的中点．

（1）证明平面；

（2）设，求二面角的大小．

解答

20．（本小题满分12分）

在直角坐标系中，以为圆心的圆与直线相切．

（1）求圆的方程；

（2）圆与轴相交于两点，圆内的动点使成等比数列，

求的取值范围．

解答

21．（本小题满分12分）

设数列的首项．

（1）求的通项公式；

（2）设，证明，其中为正整数．

解答

22．（本小题满分12分）

已知函数．

（1）求曲线在点处的切线方程；

（2）设，如果过点可作曲线的三条切线，证明：．

解答