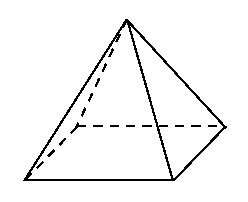
 在正四棱锥
在正四棱锥三.解答题
16.(本题满分12分)
 在正四棱锥
在正四棱锥![]() 中,
中,![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求
正四棱锥![]() 的体积
的体积![]() .
.
17.(本题满分14分)
在![]() 中,
中,![]() 分别是三个内角
分别是三个内角![]() 的对边.若
的对边.若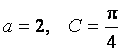 ,
,
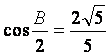 ,求
,求![]() 的面积
的面积![]() .
.
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
近年来,太阳能技术运用的步伐日益加快.2002年全球太阳电池的年生产量达到
670兆瓦,年生产量的增长率为34%. 以后四年中,年生产量的增长率逐年递增2%
(如,2003年的年生产量的增长率为36%).
(1)求2006年全球太阳电池的年生产量(结果精确到0.1兆瓦);
(2)目前太阳电池产业存在的主要问题是市场安装量远小于生产量,2006年
的实际安装量为1420兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持
在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产
量的95%),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精
确到0.1%)?
19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知函数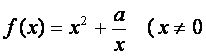 ,常数
,常数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)讨论函数![]() 的奇偶性,并说明理由.
的奇偶性,并说明理由.
20.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,
第3小题满分9分.
如果有穷数列![]() (
(![]() 为正整数)满足条件
为正整数)满足条件![]() ,
,![]() ,…,
,…,
![]() ,即
,即![]() (
(![]() ),我们称其为“对称数列”.
),我们称其为“对称数列”.
例如,数列![]() 与数列
与数列![]() 都是“对称数列”.
都是“对称数列”.
(1)设![]() 是7项的“对称数列”,其中
是7项的“对称数列”,其中![]() 是等差数列,且
是等差数列,且![]() ,
,![]() .
.
依次写出![]() 的每一项;
的每一项;
(2)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的
的
等比数列,求![]() 各项的和
各项的和![]() ;
;
(3)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的
的
等差数列.求![]() 前
前![]() 项的和
项的和![]()
![]() .
.
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分5分,
第3小题满分9分.
我们把由半椭圆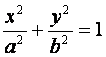
![]() 与半椭圆
与半椭圆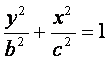
![]() 合成的曲线称作
合成的曲线称作
“果圆”,其中![]() ,
,![]() ,
,![]() .
.
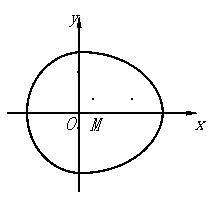 如图,设点
如图,设点![]() ,
,![]() ,
,![]() 是相应椭圆的焦点,
是相应椭圆的焦点,![]() ,
,![]() 和
和![]() ,
,![]() 是“果圆”
与
是“果圆”
与![]() ,
,![]() 轴的
轴的
交点,![]() 是线段
是线段![]() 的中点.
的中点.
(1)若![]() 是边长为1的等边三角形,求该
是边长为1的等边三角形,求该
“果圆”的方程;
(2)设![]() 是“果圆”的半椭圆
是“果圆”的半椭圆
![]() 上任意一点.求证:当
上任意一点.求证:当![]() 取得最小值时,
取得最小值时,
![]() 在点
在点![]() 或
或![]() 处;
处;
(3)若![]() 是“果圆”上任意一点,求
是“果圆”上任意一点,求![]() 取得最小值时点
取得最小值时点![]() 的横坐标.
的横坐标.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。