解答题
全国卷Ⅰ(文)
(21)(本小题满分12分)
设P是椭圆![]() +y
+y![]() =1(a>1)短轴一个端点,Q为椭圆上的一个动点,
=1(a>1)短轴一个端点,Q为椭圆上的一个动点,
求![]() 的最大值.
的最大值.
全国卷Ⅱ(文)
(21)(本小题满分为14分)
设![]() ,函数
,函数![]() 若
若![]() 的解集为A,
的解集为A,
![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
北京卷(文)
(19)(本小题共14分)
椭圆C: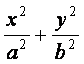 =1(a>b>0)的两个焦点为F1,F2,点P在椭圆C上,且
=1(a>b>0)的两个焦点为F1,F2,点P在椭圆C上,且
PF1⊥F1F2,|PF1|=![]() ,|PF2|=
,|PF2|=![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于A,B两点,且A,B
关于点M对称,求直线l的方程.
天津卷(文)
(21)(本小题满分14分)
已知数列{xn}满足x1=x2=1,并且
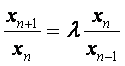 (
(![]() 为非零参数,n=2,3,4,…).
为非零参数,n=2,3,4,…).
(Ⅰ)若x1、x3、x5成等比数列,求参数λ的值;
(Ⅱ)设0<![]() <1,常数k∈N*且k≥3,证明
<1,常数k∈N*且k≥3,证明
 +…+
+…+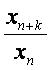 <
<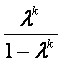 (n∈N*).
(n∈N*).
上海卷(文)
21.(本题满分16分)本题共有3个小题,第4小题满分4分.第2小题满分5分,
第3小题满分7分.
已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为
F(-![]() ,0).且右顶点为D(2,0),设点A的坐标是(1,
,0).且右顶点为D(2,0),设点A的坐标是(1,![]() ).
).
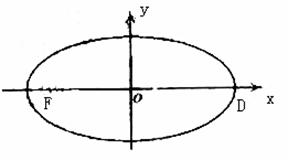
(1)求该椭圆的标准方程.
(2)若P是椭圆上的动点,求线段PA中点M的轨迹方程;
(3)过原点O的直线交椭圆于点B、C.求△ABC面积的最大值.
辽宁卷(文)
21.(本小题满分12分)
已知函数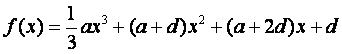 ,
,![]() ,
,
其中![]() ,设
,设![]() 为
为![]() 的极小值点,
的极小值点,![]() 为
为![]() 的极值点,
的极值点,![]() ,
,
并且![]() ,将点
,将点![]() 依次记为
依次记为![]() .
.
(1)求![]() 的值;
的值;
(2)若四边形![]() 为梯形且面积为1,求
为梯形且面积为1,求![]() 的值.
的值.
江苏卷
(21)(本小题满分14分)
设数列![]() 、
、![]() 、
、![]() 满足:
满足:![]() ,
,![]() (n=1,2,3,…),
(n=1,2,3,…),
证明![]() 为等差数列的充分必要条件是
为等差数列的充分必要条件是![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)
(n=1,2,3,…)
浙江卷(文)
(19)如图,椭圆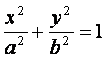 (a>b>0)与过点A(2,0)、B(0,1)的直线有
(a>b>0)与过点A(2,0)、B(0,1)的直线有
且只有一个公共点T,且椭圆的离心率e=![]()
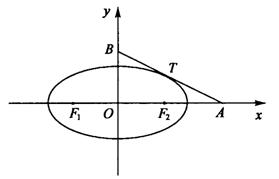
(Ⅰ)求椭圆方程;
(Ⅱ)设Fl、F2分别为椭圆的左、右焦点,求证:|AT|2=![]() |AF1|·|AF2|.
|AF1|·|AF2|.
福建卷(文)
(21)(本小题满分12分)
已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() 且
且![]() 在
在
区间![]() 上的最大值是12。
上的最大值是12。
(I)求![]() 的解析式;
的解析式;
(II)是否存在实数![]() 使得方程
使得方程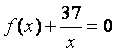 在区间
在区间![]() 内
内
有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
湖北卷(文)
20(本小题满分13分)
设数列{an}的前n项和为Sn,点(n,![]() )(n∈N*)均在函数y=3x-2的图像上。
)(n∈N*)均在函数y=3x-2的图像上。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=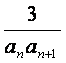 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有n∈N*都成立的最小正整数m。
对所有n∈N*都成立的最小正整数m。
湖南卷(文)
20.(本小题满分14分)
在m(m≥2)个不同数的排列p1p2…pm中,若1≤i<j≤m时pi>pj (即前面某数大
于后面某数),则称![]() 与
与![]() 构成一个逆序.一个排列的全部逆序的总数称为该排列的逆
构成一个逆序.一个排列的全部逆序的总数称为该排列的逆
序数.记排列(n+1)n(n-1)…321的逆序数为![]() ,如排列21的逆序数
,如排列21的逆序数![]() =1,排列321的逆
=1,排列321的逆
序数![]() =3,排列4321的逆序数
=3,排列4321的逆序数![]() =6.
=6.
(Ⅰ)求![]() 、
、![]() ,并写出
,并写出![]() 的表达式;
的表达式;
(Ⅱ)令![]() =
=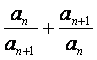 ,证明
2n<
,证明
2n<![]() +
+![]() +…+
+…+![]() <2n+3,
n=1,2,….
<2n+3,
n=1,2,….
广东卷
19.(本小题满分14分)
已知公比为q(0<q<1)的无穷等比数列{an}各项的和为9,无穷等比
数列{an2}各项的和为![]() 。
。
(Ⅰ)求数列{an}的首项a1和公比q:
(Ⅱ)对给定的k(k=1,2,…,n),设T{k}是首项为ak,公差为2ak-1的
等差数列,求数列T{2}的前10项之和:
(Ⅲ)设bi为数列![]() 的第i项,sn=b1+b2+…+bn,求sn,并求正整数
的第i项,sn=b1+b2+…+bn,求sn,并求正整数
m(m>1),使得![]()
![]() 存在且不等于零。
存在且不等于零。
(注:无穷等比数列各项的和即当n![]() 时该无穷等比数列前n项和的极限)
时该无穷等比数列前n项和的极限)
重庆卷(文)
(21)(本小题满分12分)
已知定义域为R的函数f(x)=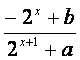 是奇函数.
是奇函数.
(Ⅰ)求a,b的值;
(Ⅱ)若对任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,
求k的取值范围.
山东卷(文)
(21)(本小题满分12分)
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点
所组成的四边形为正方形,两准线间的距离为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线l过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,
求直线l的方程.
江西卷(文)
21.(本小题满分12分)
如图,椭圆Q: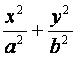 =1(a>b>0)的右焦点为F(c,0),过点F的一动直线m
=1(a>b>0)的右焦点为F(c,0),过点F的一动直线m
绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
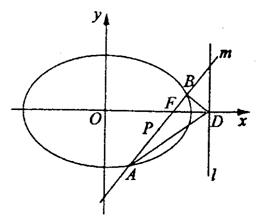
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ).
).
设轨迹H的最高点和最低点分别为M和N.当θ为何值时,△MNF为—个正三角形?
陕西卷(文)
(21)(本小题满分为12分)
如图,三定点![]() 三动点D、E、M满足
三动点D、E、M满足
![]()
![]()
(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
四川卷(文)
(21)(本大题满分12分)
已知函数![]() ,其中
,其中![]() 是
是![]() 的导函数
的导函数
(Ⅰ)对满足![]() 的一切
的一切![]() 的值,都有
的值,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() ,当实数
,当实数![]() 在什么范围内变化时,函数
在什么范围内变化时,函数![]() 的图象与
的图象与
直线![]() 只有一个公共点
只有一个公共点
安徽卷(文)
(21)(本大题满分12分)在等差数列![]() 中,
中,![]() ,前
,前![]() 项和
项和![]() 满足
满足
条件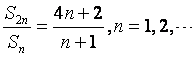 ,
,
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。