解答题

 全国卷Ⅰ(文)

(19) (本小题满分12分)

A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验,每个试验组由4只小

白鼠组成,其中2只服用A,另2只服用B,然后观察疗效,若在一个试验组中,服用A有

效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A

有效的概率为,服用B有效的概率为.

(Ⅰ)求一个试验组为甲类组的概率；

(Ⅱ)观察3个试验组，求这3个试验组中至少有一个甲类组的概率.

解答

全国卷Ⅱ(文)

（19）（本小题满分１２分）

某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，

再从每箱中任意抽取2件产品进行检验。设取出的第一、二、三箱中

分别有0件、1件、2件二等品，其余为一等品。

   （I）求取6件产品中有1件产品是二等品的概率。

   （II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购

买这批产品，求这批产品被用户拒绝的概率。

      解答

北京卷(文)

(17)(本小题共14分)

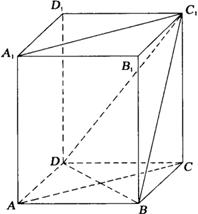
如图，ABCD-A₁B₁C₁D₁是正四棱柱.

(Ⅰ)求证：BD⊥平面ACC₁A₁；

(Ⅱ)若二面角C₁-BD-C的大小为60°，求异面直线BC₁与AC所成角的大小.

解答

天津卷(文)

(19)(本小题满分12分)

    如图，在五面体ABCDEF中，点O是矩形ABCD的对角线的交点，

面CDE是等边三角形，棱EFBC.

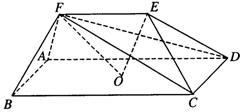
(Ⅰ)证明FO∥平面CDE；

(Ⅱ)设BC=CD，证明EO⊥平面CDF

 解答

上海卷(文)

19.（本题满分14分）本题共有2个小题，第1小题满分5分. 第2小题满分9分.

在直三棱柱ABC-A₁B₁C₁中，∠ABC=90°.AB=BC=1，

（1）求异面直线B₁C₁与AC所成角的大小；

（2）若直线A₁C与平面ABC所成角为45°.求三棱柱A₁-ABC的结果.

解答

辽宁卷(文)

19．（本小题满分12分）

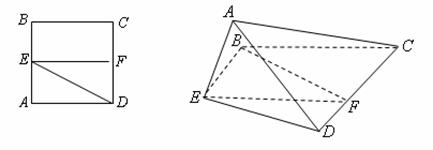
已知正方形，分别是边的中点，将沿折起，

如图所示，记二面角的大小为（）．

（1）证明平面；

（2）若为正三角形，试判断点在平面内的射影是否在直线

上，证明你的结论，并求角的余弦值.

解答

     江苏卷

（19）（本小题满分14分，第一小问满分4分，第二小问满分5分，

     第三小问满分5分）

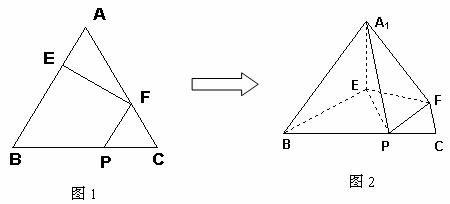
　　　在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足

     AE:EB＝CF:FA＝CP:PB＝1:2（如图1）。将△AEF沿EF折起到的位置，

     使二面角A₁－EF－B成直二面角，连结A₁B、A₁P（如图2）

   （Ⅰ）求证：A₁E⊥平面BEP；

（Ⅱ）求直线A₁E与平面A₁BP所成角的大小；

（Ⅲ）求二面角B－A₁P－F的大小（用反三角函数表示）

解答

浙江卷(文)

(17)如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，

PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点．

    (Ⅰ)求证：PB⊥DM；

    (Ⅱ)求BD与平面ADMN所成的角．

解答

福建卷(文)

（19）（本小题满分12分）

       如图，四面体ABCD中，O、E分别是BD、BC的中点，

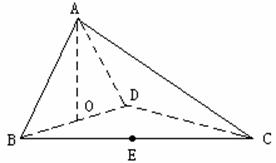
       （I）求证：平面BCD；

       （II）求异面直线AB与CD所成角的大小；

       （III）求点E到平面ACD的距离。

解答

湖北卷(文)

18．（本小题满分12分）

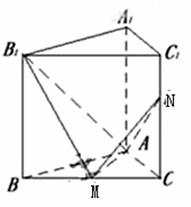
如图，已知正三棱柱ABC—A₁B₁C₁的侧棱长和底面边长为1，M是底面BC边上的中点，

N是侧棱CC₁上的点，且CN=2C₁N。

（Ⅰ）求二面角B₁—AM—N的平面角的余弦值；

（Ⅱ）求点B₁到平面AMN的距离。

解答

湖南卷(文)

18．(本小题满分14分)

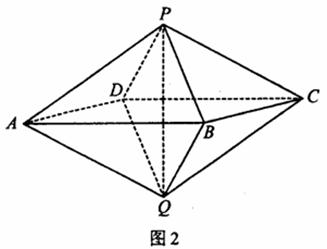
    如图2，已知两个正四棱锥P-ABCD与Q-ABCD的高都为2，AB=4．

    (Ⅰ)证明PQ⊥平面ABCD；

    (Ⅱ)求异面直线AQ与PB所成的角；

    (Ⅲ)求点P到平面QAD的距离．

      解答

广东卷

17．（本小题满分14分）

    如图所示，AF、DE分别是⊙、⊙₁的直径。AD与两圆所在的平面均

垂直，AD=8，BC是⊙的直径，AB=AC=6，OE//AD。

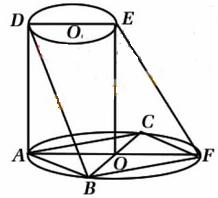
    （Ⅰ）求二面角B-AD-F的大小；

    （Ⅱ）求直线BD与EF所成的角。

解答

重庆卷(文)

(19)（本小题满分12分）

设函数f（x）=x³－3ax²+3bx的图象与直线12x+y-1=0相切于点（1，－11）.

(Ⅰ)求a，b的值；

(Ⅱ)讨论函数f（x）的单调性.

解答

山东卷(文)

（19）（本小题满分12分）

盒中装着标有数字1，2，3，4的卡片各2张，从盒中任意任取3张，

每张卡片被抽出的可能性都相等，求：

(Ⅰ)抽出的3张卡片上最大的数字是4的概率；

(Ⅱ)抽出的3张中有2张卡片上的数字是3的概率；

(Ⅲ)抽出的3张卡片上的数字互不相同的概率.

解答

江西卷(文)

19．(本小题满分12分)

    在锐角△ABC中，角A、B、C所对的边分别为a、b、c，已知sinA=，

    (1)求tan²+sin²的值；

    (2)若a=2，S_△ABC=，求b的值．

解答

 陕西卷(文)

（１９）（本小题满分１２分）

如图，点A在直线上的射影为点B在上的射影为

已知求：

       （I）直线AB分别与平面所成角的大小；

       （II）二面角的大小。

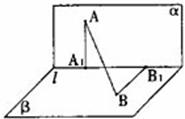
(第19题图)

解答

 四川卷(文)

（19）（本大题满分12分）

某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与

“不合格”，两部分考核都是“合格”则该课程考核“合格”，甲、乙、

丙三人在理论考核中合格的概率分别为；在实验考核中合格的概

率分别为，所有考核是否合格相互之间没有影响

（Ⅰ）求甲、乙、丙三人在理论考核中至少有两人合格的概率；

（Ⅱ）求这三人该课程考核都合格的概率。（结果保留三位小数）

解答

 安徽卷(文)

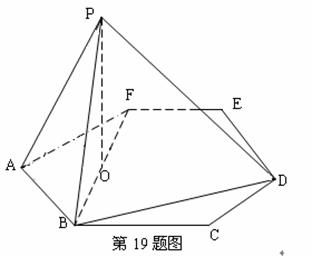
（19）（本大题满分12分）如图，P是边长为1的正六边形ABCDEF所在平面外一点，

，P在平面ABC内的射影为BF的中点O。

（Ⅰ）证明⊥；

（Ⅱ）求面与面所成二面角的大小。

解答