｝为等比数列,a
=2，a
+a
=
.求｛a
｝的通项公式.解答题
全国卷Ⅰ(文)
(17)(本小题满分12分)
已知｛a｝为等比数列,a=2，a+a=.求｛a｝的通项公式.
全国卷Ⅱ(文)
（17）（本小题满分１２分）
在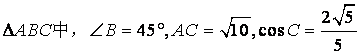
,求
（1）
(2)若点
北京卷(文)
(15)(本小题共12分)
已知函数f(x)=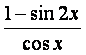
.
(Ⅰ)求f(x)的定义域；
(Ⅱ)设α是第四象限的角，且tanα=
-
，求f(α)的值.
天津卷(文)
（17）(本小题满分12分)
已知tanα+cotα=
，α∈(
，
)，求cos2α和sin(2α+)的值.
上海卷(文)
(17)（本题满分12分）
已知α是第一象限的角，且cosα=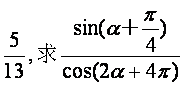
的值.
辽宁卷(文)
(17) (本小题满分12分)
已知函数
，
.求:
(I)
函数
的最大值及取得最大值的自变量
的集合；
(II)
函数的单调增区间.
江苏卷
（17）（本小题满分12分，第一小问满分5分，第二小问满分7分）
已知三点P（5，2）、
（－6，0）、
（6，0）.
（Ⅰ）求以
、
为焦点且过点P的椭圆的标准方程；
（Ⅱ）设点P、
、
关于直线y＝x的对称点分别为
、
、
，
求以
、
为焦点且过点
的双曲线的标准方程。
浙江卷(文)
(15)若Sn是公差不为0的等差数列{an}的前n项和，且S1，S2，S4成等比数列．
(Ⅰ)求数列S1，S2，S4的公比；
(Ⅱ)若S2=4，求{an}的通项公式．
福建卷(文)
（17）（本小题满分12分）
已知函数
=sin
x+
sinxcosx，x∈R
（I）求函数
的最小正周期和单调增区间；
（II）函数的图象可以由函数
的图象经过怎样的变换得到？
湖北卷(文)
16.（本小题满分12分）
设向量a=（sinx，cos x），b=（cosx，cosx），x∈R，函数f（x）=a（a+b）。
（Ⅰ）求函数f（x）的最大值与最小正周期；
（Ⅱ）求使不等式f（x）≥
成立的x的取值集合。
湖南卷(文)
16．(本小题满分12分)
已知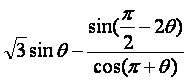
·cosθ=1,θ∈(0，π)，求θ的值．
广东卷
15．（本小题满分14分）
已知函数
（Ⅰ）求f(x)的最小正周期：
（Ⅱ）求f(x)的最大值和最小值：
（Ⅲ）若
求sin2
的值。
重庆卷(文)
（17）（本小题满分13分）
甲、乙、丙三人在同一办公室工作，办公室里只有一部电话机，
设经该机打进的电话
是打给甲、乙、丙的概率依次为
、
、
.若在一段时间内打进
三个电话，且各个电话相互独立.
求：
(Ⅰ)这三个电话是打给同一个人的概率；
(Ⅱ)这三个电话中恰有两个是打给甲的概率.
山东卷(文)
（17）（本小题满分12分）
设函数f(x)=
(Ⅰ)求f(x)的单调区间；
(Ⅱ) 讨论f(x)的极值.
江西卷(文)
17．(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c在x=-
与x=1时都取得极值．
(1)求a、b的值及函数f(x)的单调区间；
(2)若对x∈［-1，2］，不等式f(x)＜c2恒成立，求c的取值范围．
陕西卷(文)
17．（本小题满分12分）
甲，乙，丙三人投篮，投进的概率分别是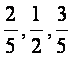
。现3人各投篮1次，求
（Ⅰ）3人都投进的概率；
（Ⅱ）3人中恰有2人投进的概率。
四川卷(文)
（17）（本大题满分12分）
数列
的前
项和记为
（Ⅰ）求
的通项公式；
（Ⅱ）等差数列
的各项为正，其前
项和为
，且
，
又
成等比数列，求
安徽卷(文)
（17）（本大题满分12分）已知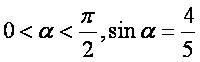
（Ⅰ）求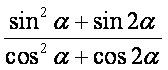
的值；
（Ⅱ）求
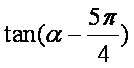的值。
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。