解答题
(17)(本小题满分12分)
已知函数![]() =sin
=sin![]() x+
x+![]() sinxcosx,x∈R
sinxcosx,x∈R
(I)求函数![]() 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(II)函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
(18)(本小题满分12分)
每次抛掷一枚骰子(六个面上分别标以数字![]()
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
(19)(本小题满分12分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,
![]()
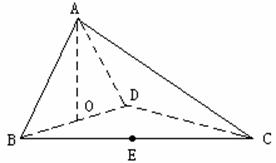
(I)求证:![]() 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
(20)(本小题满分12分)
已知椭圆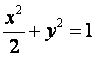 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(I)求过点O、F,并且与椭圆的左准线![]() 相切的圆的方程;
相切的圆的方程;
(II)设过点F的直线交椭圆于A、B两点,并且线段AB的
中点在直线![]() 上,求直线AB的方程。
上,求直线AB的方程。
(21)(本小题满分12分)
已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() 且
且![]() 在
在
区间![]() 上的最大值是12。
上的最大值是12。
(I)求![]() 的解析式;
的解析式;
(II)是否存在实数![]() 使得方程
使得方程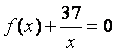 在区间
在区间![]() 内
内
有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(22)(本小题满分14分)
已知数列![]() 满足
满足![]()
(I)证明:数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式;
的通项公式;
(II)若数列![]() 满足
满足![]() 证明
证明![]() 是等差数列。
是等差数列。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。