三、解答题

（15）（本小题共12分）

已知函数f（x）=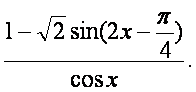

（Ⅰ）求f（x）的定义域；

（Ⅱ）设α是第四象限的角，且tanα=－求f（α）的值.

解答

（16）（本小题共13分）

 已知函数f（x）=ax³+bx²+cx在点x₀处取得极大值5，其导函数y=f′（x）

的图象经过点（1，0），（2，0），如图所示，求：

（Ⅰ）x₀的值；

（Ⅱ）a，b，c的值.

^解答

（17）（本小题共14分）

如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，

且PA=AB，点E是PD的中点.

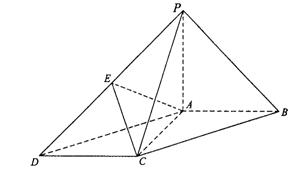
（Ⅰ）求证：AC⊥PB；

（Ⅱ）求证：PB∥平面AEC；

（Ⅲ）求二面角E-AC-B的大小.

解答

(18)(本小题共13分)

    某公司招聘员工，指定三门考试课程，有两种考试方案．

    方案一：考试三门课程，至少有两门及格为考试通过；

    方案二：在三门课程中，随机选取两门，这两门都及格为考试通过．

    假设某应聘者对三门指定课程考试及格的概率分别是a，b，c，且三门课程

考试是否及格相互之间没有影响．

(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率；

(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小．(说明理由)

解答

(19)(本小题共14分)

    已知点M（-2，0)，N(2，0)，动点P满足条件|PM|-|PN|=2.记动点P的

轨迹为W.

    (Ⅰ)求W的方程；

    (Ⅱ)若A，B是W上的不同两点，O是坐标原点，求的最小值．

解答

(20)(本小题共14分)

    在数列{a_n}中，若a₁，a₂是正整数，且a_n=|a_n-1-a_n-2|,n=3，4，5，…，

则称{a_n}为“绝对差数列”.

    (Ⅰ)举出一个前五项不为零的“绝对差数列”(只要求写出前十项)；

    (Ⅱ)若“绝对差数列”{a_n}中，a₂₀=3，a₂₁=0，数列{b_n}满足b_n=a_n+ a_n+1

+ a_n+2，n=1，2，3，…，分别判断当n→∞时，a_n与b_n的极限是否存在，如果存

在，求出其极限值；

（Ⅲ）证明：任何“绝对差数列”中总含有无穷多个为零的项.

       解答