解答题

（17）（本题满分12分）

在ΔABC中，角A、B、C所对的边分别为a、b、c，且。

（Ⅰ）求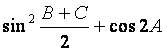的值；

（Ⅱ）若，求bc的最大值。

解答

（18） （本题满分12分）

盒子中有大小相同的球10个，其中标号为1的球3个，标号为2的球4个，

标号为5的球3个，第一次从盒子中任取1个球，放回后第二次再任取1个球

（假设取到每个球的可能性都相同）。记第一次与第二次取到球的标号之和为ε。

（Ⅰ）求随机变量ε的分布列；

（Ⅱ）求随机变量ε的期望Eε。

解答

（19）（本题满分12分）

如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，

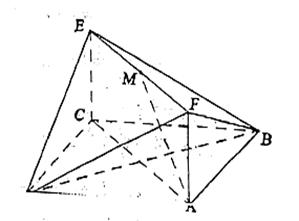   AB=，AF=1，M是线段EF的中点。

  （Ⅰ）求证AM∥平面BDE；

  （Ⅱ）求二面角A—DF—B的大小；

    解答

（20）（本题满分12分）

   设曲线≥0）在点M（t,c^--1）处的切线与x轴y轴所围成

 的三角表面积为S（t）。

   （Ⅰ）求切线的方程；

（Ⅱ）求S（t）的最大值。

      解答

（21）（本题满分12分）

已知双曲线的中心在原点，右顶点为A（1，0）点P、Q在双

曲线的右支上，支M（m,0）到直线AP的距离为1。

（Ⅰ）若直线AP的斜率为k，且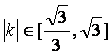，求实数m的

  取值范围；

（Ⅱ）当时，ΔAPQ的内心恰好是点M，求此双曲

线的方程。

解答

（22）（本题满分14分）

  如图，ΔOBC的在个顶点坐标分别为（0,0）、（1,0）、（0,2）,

设P为线段BC的中点,P₂为线段CO的中点,P₃为线

段OP₁的中点,对于每一个正整数n,P_n+3为线段P_nP_n+1的

中点,令P_n的坐标为(x_n,y_n),

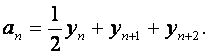
  （Ⅰ）求及;

（Ⅱ）证明

 (Ⅲ)若记证明是等比数列.

       解答