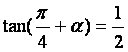 ,(1)求
,(1)求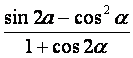 的值。
的值。解答题
17. (本小题满分12分)
已知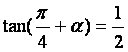 ,(1)求
,(1)求![]() 的值;(2)求
的值;(2)求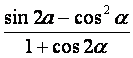 的值。
的值。
18. (本小题满分12分)
从4名男生和2名女生中任选3人参加演讲比赛,设随机变量![]() 表示
表示
所选3人中女生的人数。
(1)求![]() 的分布列;
的分布列;
(2)求![]() 的数学期望;
的数学期望;
(3)求“所选3人中女生人数![]() ”的概率。
”的概率。
19. (本小题满分12分)
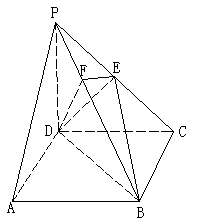
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,
PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)证明PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C—PB—D的大小。
20. (本小题满分12分)
已知函数![]() 在
在![]() 处取得极值。
处取得极值。
(1)讨论![]() 和
和![]() 是函数
是函数![]() 的极大值还是极小值;
的极大值还是极小值;
(2)过点![]() 作曲线
作曲线![]() 的切线,求此切线方程。
的切线,求此切线方程。
21. (本小题满分12分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:
![]() ,
,
![]() ,其中a为常数,k为非零常数。
,其中a为常数,k为非零常数。
(1)令![]()
![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(2)求数列![]() 的通项公式;
的通项公式;
(3)当![]() 时,求
时,求![]() 。
。
22. (本小题满分14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(![]() )
)
的准线![]() 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点。
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;
(2)若![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)设![]() (
(![]() ),过点P且平行于准线
),过点P且平行于准线![]() 的直线与椭圆相交于
的直线与椭圆相交于
另一点M,证明![]() 。
。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。