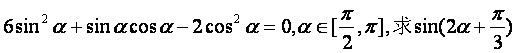解答题

17．（本小题满分12分）

       已知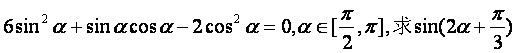的值.

  解答

18．（本小题满分12分）

     如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，AC与BD交于点E，

CB与CB₁交于点F.

（I）求证：A₁C⊥平BDC₁；

（II）求二面角B—EF—C的大小（结果用反三角函数值表示）.

　          解答

19．（本小题满分12分）

    如图，在Rt△ABC中，已知BC=a.若长为2a的线段PQ以点A为中点，

问的夹角θ取何值时的值最大？并求出这个最大值.

　　　　　　　　　　解答

20．（本小题满分12分）

直线的右支交于不同的两点A、B.

（Ⅰ）求实数k的取值范围；

（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？

若存在，求出k的值；若不存在，说明理由.

　解答

21．（本小题满分12分）

为防止某突发事件发生，有甲、乙、丙、丁四种相互独立的预防措施

可供采用，单独采用甲、乙、丙、丁预防措施后此突发事件不发生的

概率（记为P）和所需费用如下表：

预防方案可单独采用一种预防措施或联合采用几种预防措施，在总费用不超

过120万元的前提下，请确定一个预防方案，使得此突发事件不发生的概率最大.

 解答

22．（本小题满分14分）

已知的图象相切.

（Ⅰ）求b与c的关系式（用c表示b）；

（Ⅱ）设函数内有极值点，求c的取值范围.

 解答