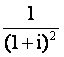 等于(
)
等于(
)福建(理)
一、选择题(每小题5分)
1.复数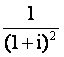 等于(
)
等于(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.对于向量![]() 和实数
和实数![]() ,下列命题中真命题是(
)
,下列命题中真命题是(
)
A.若![]() ,则
,则![]() 或
或![]() B.若
B.若![]() ,则
,则![]() 或
或![]()
C.若![]() ,则
,则![]() 或
或![]() D.若
D.若![]() ,则
,则![]()
二、填空题(每小题4分)
16.中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.
如果集合![]() 中元素之间的一个关系“
中元素之间的一个关系“![]() ”满足以下三个条件:
”满足以下三个条件:
(1)自反性:对于任意![]() ,都有
,都有![]() ;
;
(2)对称性:对于![]() ,若
,若![]() ,则有
,则有![]() ;
;
(3)传递性:对于![]() ,若
,若![]() ,
,![]() ,则有
,则有![]() .
.
则称“![]() ”是集合
”是集合![]() 的一个等价关系.例如:“数的相等”是等价关系,
的一个等价关系.例如:“数的相等”是等价关系,
而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______.
浙江(理)
二、填空题(每小题4分)
(11)已知复数![]() ,
,![]() ,则复数
,则复数![]() .
.
(14)某书店有11种杂志,2元1本的8种,1元1本的3种,小张用10元钱买杂志
(每种至多买一本,10元钱刚好用完),则不同买法的种数是 (用数字作答).
天津(理)
一、选择题(每小题5分)
1.![]() 是虚数单位,
是虚数单位,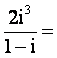 ( )
( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
9.设![]() 均为正数,且
均为正数,且![]() ,
,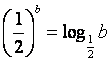 ,
,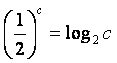 .则( )
.则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分)
16.如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,
要求最多使用3种颜色且相邻的两个格子颜色不同,
则不同的涂色方法共有 种(用数字作答).
辽宁(理)
一、选择题(每小题5分)
1.设集合![]() ,
,![]() ,
,![]() ,则
,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若向量![]() 与
与![]() 不共线,
不共线,![]() ,且
,且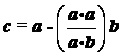 ,则向量
,则向量![]() 与
与![]() 的夹角为(
)
的夹角为(
)
A.0
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分)
16.将数字1,2,3,4,5,6拼成一列,记第![]() 个数为
个数为![]() ,
,
若![]() ,
,![]() ,
,![]() ,
,![]() ,则不同的排列方法有
种(用数字作答).
,则不同的排列方法有
种(用数字作答).
重庆(理)
一、选择题(每小题5分)
8.设正数![]() 满足
满足![]() ,则
,则 ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分)
11.复数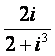 的虚部为______.
的虚部为______.
15.某校要求每位学生从![]() 门课程中选修
门课程中选修![]() 门,其中甲、乙两门课程不能都选,
门,其中甲、乙两门课程不能都选,
则不同的选课方程有______种.(以数字作答)
湖南(理)
一、选择题(每小题5分)
1.复数 等于(
)
等于(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设![]() 是两个集合,则“
是两个集合,则“![]() ”是“
”是“![]() ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
10.设集合![]() ,
, ![]() 都是
都是![]() 的含两个元素的子集,
的含两个元素的子集,
且满足:对任意的![]() ,
,![]() (
(![]() ,
,![]() ),
),
都有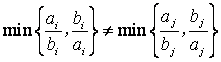 (
(![]() 表示两个数
表示两个数![]() 中的较小者),
中的较小者),
则![]() 的最大值是(
)
的最大值是(
)
A.10 B.11 C.12 D.13
湖北(理)
一、选择题(每小题5分)
3.设![]() 和
和![]() 是两个集合,定义集合
是两个集合,定义集合![]() ,如果
,如果![]() ,
,
![]() ,那么
,那么![]() 等于( )
等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.已知![]() 和
和![]() 是两个不相等的正整数,且
是两个不相等的正整数,且![]() ,则
,则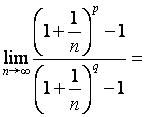 (
)
(
)
A.0
B.1 C.![]() D.
D.![]()
二、填空题(每小题5分)
12.复数![]() ,且
,且![]() ,若
,若![]() 是实数,则有序实数对
是实数,则有序实数对![]() 可以
可以
是 .(写出一个有序实数对即可)
江苏
一、选择题(每小题5分)
2.已知全集![]() ,
,![]() ,
,![]() ,则
,则![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
广东(理)
一、选择题(每小题5分)
2.若复数![]() 是纯虚数(
是纯虚数(![]() 是虚数单位,
是虚数单位,![]() 是实数),则
是实数),则![]() (
)
(
)
A.2
B.![]() C.
C.![]() D.
D.![]()
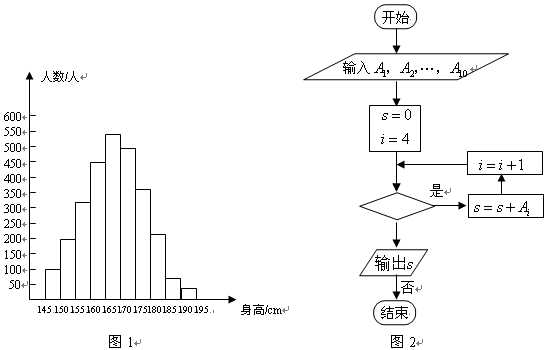
6.图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的
学生人数依次记为![]() (如
(如![]() 表示身高(单位:cm)在
表示身高(单位:cm)在![]() 内的学生人数).
内的学生人数).
图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计
身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中
的判断框内应填写的条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

7.图3是某汽车维修公司的维修点环形分布图.公司在年初分配给![]() 四个
四个
维修点某种配件各50件.在使用前发现需将![]() 四个维修点的这批配件分别
四个维修点的这批配件分别
调整为![]() ,
,![]() ,
,![]() ,
,![]() 件,但调整只能在相邻维修点之间进行,那么要完成上述
件,但调整只能在相邻维修点之间进行,那么要完成上述
调整,最少的调动件次(![]() 件配件从一个维修点调整到相邻
件配件从一个维修点调整到相邻
维修点的调动件次为![]() )为( )
)为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设![]() 是至少含有两个元素的集合,在
是至少含有两个元素的集合,在![]() 上定义了一个二元运算“*”(即对任意
上定义了一个二元运算“*”(即对任意
的![]() ,对于有序元素对(
,对于有序元素对(![]() ),在
),在![]() 中有唯一确定的元素
中有唯一确定的元素![]() 与之对应).
与之对应).
若对任意的![]() ,有
,有![]()
![]() ,则对任意的
,则对任意的![]() ,下列等式中不恒成立
,下列等式中不恒成立
的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(每小题5分)
10.若向量![]() 满足
满足![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() .
.
北京(理)
一、选择题(每小题5分)
4.已知![]() 是
是![]() 所在平面内一点,
所在平面内一点,![]() 为
为![]() 边中点,且
边中点,且![]() ,那么( )
,那么( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.记者要为5名志愿都和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但
不排在两端,不同的排法共有( )
A.1440种 B.960种 C.720种 D.480种
二、填空题(每小题5分)
9.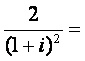 .
.
三、解答题
20.已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素
中的元素
构成两个相应的集合:
![]() ,
,![]() .
.
其中![]() 是有序数对,集合
是有序数对,集合![]() 和
和![]() 中的元素个数分别为
中的元素个数分别为![]() 和
和![]() .
.
若对于任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(I)检验集合![]() 与
与![]() 是否具有性质
是否具有性质![]() 并对其中具有性质
并对其中具有性质![]() 的集合,
的集合,
写出相应的集合![]() 和
和![]() ;
;
(II)对任何具有性质![]() 的集合
的集合![]() ,证明:
,证明: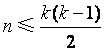 ;
;
(III)判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
上海(理)
一、填空题(每小题4分)
4.方程 ![]() 的解是
.
的解是
.
9.对于非零实数![]() ,以下四个命题都成立:
,以下四个命题都成立:
① 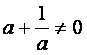 ;
②
;
② ![]() ;
;
③
若![]() ,则
,则![]() ;
④
若
;
④
若![]() ,则
,则![]() .
.
那么,对于非零复数![]() ,仍然成立的命题的所有序号是
.
,仍然成立的命题的所有序号是
.
二.选择题(每小题4分)
12.已知![]() ,且
,且![]() (
(![]() 是虚数单位)是实系数一元二次方程
是虚数单位)是实系数一元二次方程
![]() 的两个根,那么
的两个根,那么![]() 的值分别是( )
的值分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
14.直角坐标系![]() 中,
中,![]() 分别是与
分别是与![]() 轴正方向同向的单位向量.在直角三角形
轴正方向同向的单位向量.在直角三角形
![]() 中,若
中,若![]() ,则
,则![]() 的可能值个数是( )
的可能值个数是( )
A.1 B.2 C.3 D.4
山东(理)
一、选择题(每小题5分)
2、已知集合![]() ,
,![]() 则
则![]() (
)
(
)
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(9)下列各小题中,![]() 是
是![]() 的充要条件的是(
)
的充要条件的是(
)
 ①
①![]() :
:![]() 或
或![]() ;
;![]() :
:![]() 有两个不同的零点.
有两个不同的零点.
② ;
;![]() 是偶函数.
是偶函数.
③![]() ;
;![]() .
.
④![]() ;
;![]() .
.
A.①② B.②③
C.③④ D.①④
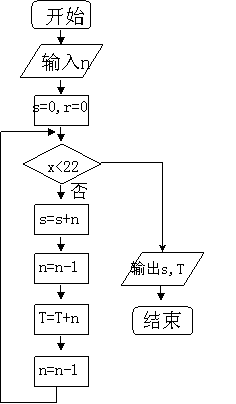
(10)阅读右边的程序框图,若输入的![]() 是100,
是100,
则输出的变量![]() 和
和![]() 的值依次是(
)
的值依次是(
)
A.2500,2500 B.2550,2550
C.2500,2550 D.2550,2500`
江西(理)
一、选择题(每小题5分)
1.化简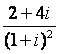 的结果是( )
的结果是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.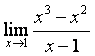 ( )
( )
A.等于![]() B.等于
B.等于![]() C.等于
C.等于![]() D.不存在
D.不存在
6.若集合![]() ,
,![]() ,
,
则![]() 中元素的个数为( )
中元素的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
陕西(理)
一、选择题(每小题5分)
1.在复平面内,复数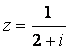 对应的点位于(
)
对应的点位于(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.给出如下三个命题:
①四个非零实数![]() 依次成等比数列的充要条件是
依次成等比数列的充要条件是![]() ;
;
②设![]() ,且
,且![]() ,若
,若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() 是偶函数.
是偶函数.
其中不正确命题的序号是( )
A.①②③ B.①② C.②③ D.①③
12.设集合![]() ,在
,在![]() 上定义运算
上定义运算![]() 为:
为:![]() ,其中
,其中![]() 为
为![]()
被4除的余数,![]() ,则满足关系式
,则满足关系式![]() 的
的![]() 的个数为(
)
的个数为(
)
A.4 B.3 C.2 D.1
二、填空题(每小题4分)
13. .
.
15.如图,平面内有三个向量![]() ,其中
,其中![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 与
与![]() 的
的
夹角为![]() ,且
,且![]() ,
,![]() .若
.若![]() ,
,
则![]() 的值为
的值为 .
.
安徽(理)
一、选择题(每小题5分)
4.若![]() 为实数,
为实数, ,则
,则![]() 等于(
)
等于(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若![]() ,则
,则![]() 的元素个数为(
)
的元素个数为(
)
A.0 B.1 C.2 D.3
二、填空题(每小题4分)
12.若 的展开式中含有常数项,则最小的正整数
的展开式中含有常数项,则最小的正整数![]() 等于
.
等于
.
四川(理)
一、选择题(每小题5分)
(1)复数 的值是(
)
的值是(
)
(A)0 (B)1 (C)-1 (D)1
(3)
(A)0 (B)1
(C)![]() (D)
(D)![]()
(7)设A{a,1},B{2,b},C{4,5},为坐标平面上三点,O为坐标原点,若
![]() 上的投影相同,则a与b满足的关系式为(
)
上的投影相同,则a与b满足的关系式为(
)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
海南宁夏(理)
一、选择题(每小题5分)
2.已知平面向量![]() ,则向量
,则向量 ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.如果执行右面的程序框图,那么输出的![]() ( )
( )
A.2450 B.2500
C.2550 D.2652

二、填空题(每小题5分)
15.![]() 是虚数单位,
是虚数单位, .(用
.(用![]() 的形式表示,
的形式表示,![]() )
)
16.某校安排5个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少
安排一个班,不同的安排方法共有 种.(用数字作答)
三、解答题
22.请考生在![]() 三题中任选一题作答,如果多做,则按所做的第一题记分.
三题中任选一题作答,如果多做,则按所做的第一题记分.
作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.
 22.A(本小题满分10分)选修4-1:几何证明选讲
22.A(本小题满分10分)选修4-1:几何证明选讲
如图,已知![]() 是
是![]() 的切线,
的切线,![]() 为切点,
为切点,![]() 是
是![]() 的割线,与
的割线,与![]() 交于
交于![]() 两点,
两点,
圆心![]() 在
在![]() 的内部,点
的内部,点![]() 是
是![]() 的中点.
的中点.
(Ⅰ)证明![]() 四点共圆;
四点共圆;
(Ⅱ)求![]() 的大小.
的大小.
22.B(本小题满分10分)选修4-4:坐标系与参数方程
![]() 和
和![]() 的极坐标方程分别为
的极坐标方程分别为![]() .
.
(Ⅰ)把![]() 和
和![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)求经过![]() ,
,![]() 交点的直线的直角坐标方程.
交点的直线的直角坐标方程.
22.C(本小题满分10分)选修![]() ;不等式选讲
;不等式选讲
设函数![]() .
.
(I)解不等式![]() ;
;
(II)求函数![]() 的最小值.
的最小值.
全国卷(Ⅰ)理
一、选择题(每小题5分)
(2)设![]() 是实数,且
是实数,且 是实数,则
是实数,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(3)已知向量![]() ,
,![]() ,则
,则![]() 与
与![]() ( )
( )
A.垂直 B.不垂直也不平行 C.平行且同向 D.平行且反向
(5)设![]() ,集合
,集合 ,则
,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
全国卷(Ⅱ)理
一、选择题(每小题5分)
3.设复数![]() 满足
满足![]() ,则
,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列四个数中最大的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,
要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有( )
A.40种 B.60种 C.100种 D.120种
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。