三、解答题
20.已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素
中的元素
构成两个相应的集合:
![]() ,
,![]() .
.
其中![]() 是有序数对,集合
是有序数对,集合![]() 和
和![]() 中的元素个数分别为
中的元素个数分别为![]() 和
和![]() .
.
若对于任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(I)检验集合![]() 与
与![]() 是否具有性质
是否具有性质![]() 并对其中具有性质
并对其中具有性质![]() 的集合,
的集合,
写出相应的集合![]() 和
和![]() ;
;
(II)对任何具有性质![]() 的集合
的集合![]() ,证明:
,证明: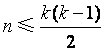 ;
;
(III)判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(I)解:集合![]() 不具有性质
不具有性质![]() .
.
集合![]() 具有性质
具有性质![]() ,其相应的集合
,其相应的集合![]() 和
和![]() 是
是![]() ,
,
![]() .
.
(II)证明:首先,由![]() 中元素构成的有序数对
中元素构成的有序数对![]() 共有
共有![]() 个.
个.
因为![]() ,所以
,所以![]() ;
;
又因为当![]() 时,
时,![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,
![]() .
.
从而,集合![]() 中元素的个数最多为
中元素的个数最多为 ,
,
即 .
.
(III)解:![]() ,证明如下:
,证明如下:
(1)对于![]() ,根据定义,
,根据定义,![]() ,
,![]() ,且
,且![]() ,从而
,从而![]() .
.
如果![]() 与
与![]() 是
是![]() 的不同元素,那么
的不同元素,那么![]() 与
与![]() 中至少有一个不成立,
中至少有一个不成立,
从而![]() 与
与![]() 中也至少有一个不成立.
中也至少有一个不成立.
故![]() 与
与![]() 也是
也是![]() 的不同元素.
的不同元素.
可见,![]() 中元素的个数不多于
中元素的个数不多于![]() 中元素的个数,即
中元素的个数,即![]() ,
,
(2)对于![]() ,根据定义,
,根据定义,![]() ,
,![]() ,且
,且![]() ,从而
,从而![]() .
.
如果![]() 与
与![]() 是
是![]() 的不同元素,那么
的不同元素,那么![]() 与
与![]() 中至少有一个不成立,
中至少有一个不成立,
从而![]() 与
与![]() 中也不至少有一个不成立,
中也不至少有一个不成立,
故![]() 与
与![]() 也是
也是![]() 的不同元素.
的不同元素.
可见,![]() 中元素的个数不多于
中元素的个数不多于![]() 中元素的个数,即
中元素的个数,即![]() ,
,
由(1)(2)可知,![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。