一、选择题(每小题5分)
7.连接抛物线![]() 的焦点
的焦点![]() 与点
与点![]() 所得的线段与抛物线交于点
所得的线段与抛物线交于点![]() ,
,
设点![]() 为坐标原点,则三角形
为坐标原点,则三角形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.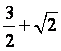
12.设椭圆 的离心率为
的离心率为 ,右焦点为
,右焦点为![]() ,
,
方程![]() 的两个实根分别为
的两个实根分别为![]() 和
和![]() ,则点
,则点![]() ( )
( )
A.必在圆![]() 上
B.必在圆
上
B.必在圆![]() 外
外
C.必在圆![]() 内
D.以上三种情形都有可能
内
D.以上三种情形都有可能
二、填空题(每小题4分)
13.在平面直角坐标系中,正方形![]() 的对角线
的对角线![]() 的两端点分别为
的两端点分别为![]() ,
,![]() ,
,
则![]() .
.
三、解答题
22.(本小题满分14分)
设动点![]() 到点
到点![]() 和
和![]() 的距离分别为
的距离分别为![]() 和
和![]() ,
,![]() ,
,
且存在常数![]() ,使得
,使得![]() .
.
 (1)证明:动点
(1)证明:动点![]() 的轨迹
的轨迹![]() 为双曲线,并求出
为双曲线,并求出![]() 的方程;
的方程;
(2)如图,过点![]() 的直线与双曲线
的直线与双曲线![]() 的右支交于
的右支交于![]() 两点.
两点.
问:是否存在![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰
为直角顶点的等腰
直角三角形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.