选择题(每小题5分)

4.设三棱柱ABC-A₁B₁C₁的体积是V，P.Q分别是侧棱AA₁.CC₁上的点，且PA=QC₁，

则四棱锥B-APQC的体积为（ ）

A.           B.         C.        D.

解答

11.不共面的四个定点到平面α的距离都相等，这样的平面α共有（ ）个

A.3           B.4                 C.6               D.7

解答

解答题

19.（本小题满分12分）

    四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，

    平面VAD⊥底面ABCD

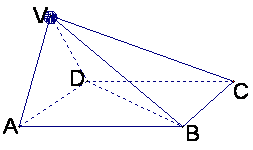    1）求证AB⊥面VAD；

    2）求面VAD与面VDB所成的二面角的大小．

   解答

(21) (本小题满分12分)

用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去

一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为

多少时,容器的容积最大?最大容积是多少?

解答