解答题
19.(本小题满分12分)
四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,
平面VAD⊥底面ABCD![]()
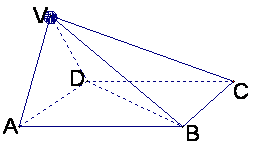 1)求证AB⊥面VAD;
1)求证AB⊥面VAD;
2)求面VAD与面VDB所成的二面角的大小.
证法一:(1)由于面VAD是正三角形,设AD的中点为E,则VE⊥AD,而
面VAD⊥底面ABCD,则VE⊥AB![]()
又面ABCD是正方形,则AB⊥CD,故AB⊥面VAD![]()
(2)由AB⊥面VAD,则点B在平面VAD内的射影是A,设VD的中点为F,连AF,BF
由△VAD是正△,则AF⊥VD,由三垂线定理知BF⊥VD,故∠AFB是面VAD与面VDB
所成的二面角的平面角![]()
设正方形ABCD的边长为a,
则在Rt△ABF中,,AB=a, AF=![]() a,tan∠AFB
=
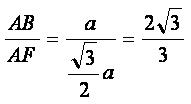
a,tan∠AFB
=
故面VAD与面VDB所成的二面角的大小为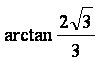
![]()
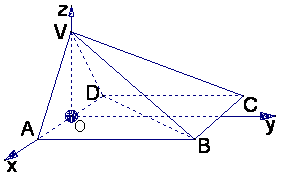
证明二:(Ⅰ)作AD的中点O,则VO⊥底面ABCD.…………1分
建立如图空间直角坐标系,并设正方形边长为1,………2分
则A(![]() ,0,0),B(
,0,0),B(![]() ,1,0),C(-
,1,0),C(-![]() ,1,0),D(-
,1,0),D(-![]() ,0,0),
,0,0),
V(0,0,![]() ),
),
 ∴
∴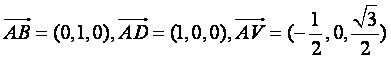 ……3分
……3分
由![]() …………4分
…………4分
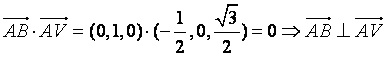 ……5分
……5分
又AB∩AV=A ∴AB⊥平面VAD…………………………6分
(Ⅱ)由(Ⅰ)得![]() 是面VAD的法向量……………………7分
是面VAD的法向量……………………7分
设![]() 是面VDB的法向量,则
是面VDB的法向量,则
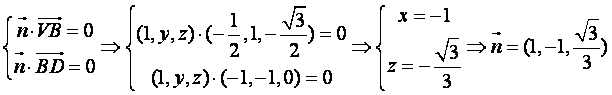 ……9分
……9分
∴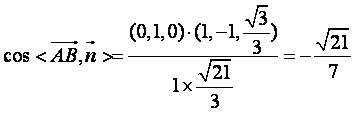 ,……………11分
,……………11分
又由题意知,面VAD与面VDB所成的二面角,所以其大小为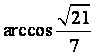 ……12分
……12分
(II)证法三:由(Ⅰ)得![]() 是面VAD的法向量…………………7分
是面VAD的法向量…………………7分
设平面VDB的方程为mx+ny+pZ+q=0,将V.B.D三点的坐标代入可得
 解之可得
解之可得 令q=
令q=![]() 则平面VDB的方程为x-y+
则平面VDB的方程为x-y+![]() Z+
Z+![]() =0
=0
故平面VDB的法向量是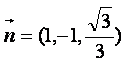 ………………………………9分
………………………………9分
∴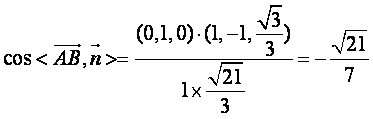 ,………………11分
,………………11分
又由题意知,面VAD与面VDB所成的二面角,所以其大小为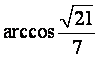 ……12分
……12分
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。