选择题

13、在下列关于直线l、m与平面α、β的命题中,真命题是(    )

   (A)若lβ且α⊥β,则l⊥α.   (B) 若l⊥β且α∥β,则l⊥α.

(C) 若l⊥β且α⊥β,则l∥α.  (D) 若α∩β=m且l∥m,则l∥α.

解答

填空题

2、设抛物线的顶点坐标为(2,0),准线方程为x=－1,则它的焦点

坐标为       .(4分) 解答

8、圆心在直线x=2上的圆C与y轴交于两点A(0, -4),B(0, -2),则

圆C的方程为           .(4分) 解答

11、教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的

本质是                                 .(4分)   解答

解答题

20、(本题满分14分) 第1小题满分6分, 第2小题满分8分

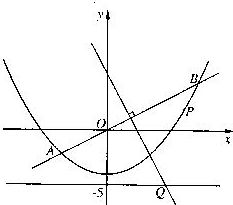  如图, 直线y=x与抛物线y=x²－4交于A、B两点, 线段AB的垂直

平分线与直线y=－5交于Q点.

 (1) 求点Q的坐标；

(2) 当P为抛物线上位于线段AB下方

(含A、B) 的动点时, 求ΔOPQ面积的最大值.

解答