|
2024年高考数学上海春17<-->2024年高考数学上海春19
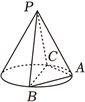
(14分)如图,$PA$、$PB$、$PC$为圆锥三条母线,$AB=AC$.
(1)证明:$PA\bot BC$;
(2)若圆锥侧面积为$\sqrt{3}\pi ,BC$为底面直径,$BC=2$,求二面角$B-PA-C$的大小.
答案:(1)证明见解答;
(2)$\pi -\arccos \dfrac{1}{5}$.
分析:(1)取$BC$中点$O$,连接$AO$,$PO$,证明$BC\bot$面$PAO$,即可证得结论;
(2)法$(i)BD\bot PA$交于$D$,连接$CD$,可得$\angle CDB$为两个平面所成的二面角的平面角,由等面积法求出$BD$的值,求出$\angle CDB$的余弦值,进而可得二面角的平面角,
法$(ii$ $)$建立空间直角坐标系,由题设求得平面$PAB$和平面$PAC$的法向量,利用向量夹角公式求得二面角的大小.
(1)证明:取$BC$中点$O$,连接$AO$,$PO$,
因为$AB=AC$,$PB=PC$,所以$AO\bot BC$,$PO\bot BC$,
又因为$PO$,$AO\subset$面$PAO$,$PO\bigcap AO=O$,
所以$BC\bot$面$PAO$,又$PA\subset$面$PAO$,
所以$PA\bot BC$;
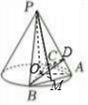
(2)解:法$(i)$由(1)可知,$BC\bot OA$,又$PO\bot$底面$ABC$,
作$PM\bot AB$,$BD\bot PA$交于$D$,连接$CD$,
由题意$\Delta PBA\cong \Delta PCA$,可得$CD\bot PA$,
所以$\angle CDB$为所求的二面角的平面角,连接$OD$,则$\angle CDB=2\angle BDO$,
因为圆锥侧面积为$\sqrt{3}\pi ,BC$为底面直径,$BC=2$,
所以底面半径为1,母线长为$\sqrt{3}$,所以$PO=\sqrt{P{A}^{2}-A{O}^{2}}=\sqrt{2}$,
$PA=\sqrt{P{O}^{2}+O{A}^{2}}=\sqrt{2+1}=\sqrt{3}$,
$AB=\sqrt{2}$,$PB=\sqrt{P{O}^{2}+O{B}^{2}}=\sqrt{3}$,$PM=\sqrt{P{B}^{2}-(\dfrac{AB}{2})^{2}}=\sqrt{3-\dfrac{1}{2}}=\dfrac{\sqrt{10}}{2}$,
$S_{\Delta PBA}=\dfrac{1}{2}\times AB\times PM=\dfrac{1}{2}\times PA\times BD$,
即$\sqrt{2}\times \dfrac{\sqrt{10}}{2}=\sqrt{3}\times BD$,解得$BD=\dfrac{\sqrt{15}}{3}$,
所以$\sin \angle BDO=\dfrac{OB}{BD}=\dfrac{1}{\dfrac{\sqrt{15}}{3}}=\dfrac{\sqrt{15}}{5}$,
所以$\cos \angle CDB=1-2\sin ^{2}\angle BDO=1-2\times (\dfrac{\sqrt{15}}{5})=-\dfrac{1}{5}$,
所以二面角$B-PA-C$的平面角为钝角,
所以二面角$B-PA-C$的大小为$\pi -\arccos \dfrac{1}{5}$.
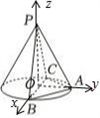
法$(ii)$由(1)可知,$BC\bot OA$,又$PO\bot$底面$ABC$,因为圆锥侧面积为$\sqrt{3}\pi ,BC$为底面直径,$BC=2$,
所以底面半径为1,母线长为$\sqrt{3}$,所以$PO=\sqrt{P{A}^{2}-A{O}^{2}}=\sqrt{2}$,
建立以$OB$为$x$轴,$OA$为$y$轴,以$OP$为$z$轴的坐标系,
则可得$P(0,0,\sqrt{2}),A(0,1,0),B(1,0,0),C(-1,0,0)$,
故$\overrightarrow{PA}=(0,1,-\sqrt{2}),\overrightarrow{PB}=(1,0,-\sqrt{2}),\overrightarrow{PC}=(-1,0,-\sqrt{2})$,
设$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$为平面$PAB$的一个法向量,
由$\overrightarrow{{n}_{1}}\bot \overrightarrow{PA}$,$\overrightarrow{{n}_{1}}\bot \overrightarrow{PB}$,
可得$\left\{\begin{array}{c}\overrightarrow{{n}_{1}}\cdot \overrightarrow{PA}=0\\ \overrightarrow{{n}_{1}}\cdot \overrightarrow{PB}=0\end{array}\right.\Rightarrow \left\{\begin{array}{c}{y}_{1}-\sqrt{2}{z}_{1}=0\\ {x}_{1}-\sqrt{2}{z}_{1}=0\end{array}\right.$,
令${x}_{1}=\sqrt{2}$,则${y}_{1}=\sqrt{2},{z}_{1}=1$,可得$\overrightarrow{{n}_{1}}=(\sqrt{2},\sqrt{2},1)$,
设$\overrightarrow{{n}_{2}}=({x}_{2},{y}_{2},{z}_{2})$为平面$PAC$的一个法向量,
由$\overrightarrow{{n}_{2}}\bot \overrightarrow{PA}$,$\overrightarrow{{n}_{2}}\bot \overrightarrow{PC}$,
可得$\left\{\begin{array}{c}\overrightarrow{{n}_{2}}\cdot \overrightarrow{PA}=0\\ \overrightarrow{{n}_{2}}\cdot \overrightarrow{PC}=0\end{array}\right.\Rightarrow \left\{\begin{array}{c}{y}_{2}-\sqrt{2}{z}_{2}=0\\ -{x}_{2}-\sqrt{2}{z}_{2}=0\end{array}\right.$,
令${x}_{2}=-\sqrt{2}$,则${y}_{2}=\sqrt{2},{z}_{2}=1$,可得$\overrightarrow{{n}_{2}}=(-\sqrt{2},\sqrt{2},1)$,
则$\cos < \overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}} > =\dfrac{\overrightarrow{{n}_{1}}\cdot \overrightarrow{{n}_{2}}}{\vert \overrightarrow{{n}_{1}}\vert \vert \overrightarrow{{n}_{2}}\vert }=\dfrac{-2+2+1}{\sqrt{5}\times \sqrt{5}}=-\dfrac{1}{5}$,
设二面角$B-PA-C$的平面角为$\theta$,由图可知$\theta$为钝角,
所以二面角$B-PA-C$的大小为$\pi -\arccos \dfrac{1}{5}$.
点评:本题考查线面垂直及线线垂直的判定,考查二面角的求法,属中档题.
2024年高考数学上海春17<-->2024年高考数学上海春19
全网搜索"2024年高考数学上海春18"相关
|

