|
2023年高考数学上海10<-->2023年高考数学上海12
(5分)某公园欲建设一段斜坡,坡顶是一条直线,斜坡顶点距水平地面的高度为4米,坡面与水平面所成夹角为$\theta$.行人每沿着斜坡向上走$1m$消耗的体力为$(1.025-\cos \theta )$,欲使行人走上斜坡所消耗的总体力最小,则$\theta =$____.
答案:$\arccos \dfrac{40}{41}$.
分析:先求出斜坡的长度,求出上坡所消耗的总体力的函数关系,求出函数的导数,利用导数研究函数的最值即可.
解:
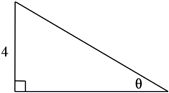
斜坡的长度为$l=\dfrac{4}{\sin \theta }$,
上坡所消耗的总体力$y=\dfrac{4}{\sin \theta }\times (1.025-\cos \theta )=\dfrac{4.1-4\cos \theta }{\sin \theta }$,
函数的导数$y\prime =\dfrac{4\sin \theta \cdot \sin \theta -(4.1-4\cos \theta )\cos \theta }{si{n}^{2}\theta }=\dfrac{4-4.1\cos \theta }{si{n}^{2}\theta }$,
由$y\prime =0$,得$4-4.1\cos \theta =0$,得$\cos \theta =\dfrac{40}{41}$,$\theta =\arccos \dfrac{40}{41}$,
由$f\prime (x) > 0$时$\cos \theta < \dfrac{40}{41}$,即$\arccos \dfrac{40}{41} < \theta < \dfrac{\pi }{2}$时,函数单调递增,
由$f\prime (x) < 0$时$\cos \theta > \dfrac{40}{41}$,即$0 < \theta < \arccos \dfrac{40}{41}$时,函数单调递减,
即$\theta =\arccos \dfrac{40}{41}$,函数取得最小值,即此时所消耗的总体力最小.
故答案为:$\theta =\arccos \dfrac{40}{41}$.
点评:本题主要考查生活的应用问题,求函数的导数,利用导数研究函数的最值是解决本题的关键,是中档题.
2023年高考数学上海10<-->2023年高考数学上海12
全网搜索"2023年高考数学上海11"相关
|

