|
2023年高考数学乙卷-理21<-->2023年高考数学乙卷-理23
[选修4-4:坐标系与参数方程](10分)
22.(10分)在直角坐标系$xOy$中,以坐标原点$O$为极点,$x$轴正半轴为极轴建立极坐标系,曲线$C_{1}$的极坐标方程为$\rho =2\sin \theta (\dfrac{\pi }{4}\leqslant \theta \leqslant \dfrac{\pi }{2})$,曲线$C_{2}:\left\{\begin{array}{l}{x=2\cos \alpha }\\ {y=2\sin \alpha }\end{array}\right.(\alpha$为参数,$\dfrac{\pi }{2} < \alpha < \pi )$.
(1)写出$C_{1}$的直角坐标方程;
(2)若直线$y=x+m$既与$C_{1}$没有公共点,也与$C_{2}$没有公共点、求$m$的取值范围.
答案:(1)$x^{2}+(y-1)^{2}=1$,$(x\in [0$,$1]$,$y\in [1$,$2])$;(2)$(-\infty ,0)\bigcup (2\sqrt{2},+\infty )$.
分析:(1)直接利用转换关系,在参数方程和直角坐标坐标方程之间进行转换;
(2)利用直线与圆的位置关系和点到直线的距离公式求出实数$m$的取值范围.
解:(1)曲线$C_{1}$的极坐标方程为$\rho =2\sin \theta (\dfrac{\pi }{4}\leqslant \theta \leqslant \dfrac{\pi }{2})$,
根据$\left\{\begin{array}{cc}x=\rho \cos \theta &\\ y=\rho \sin \theta &\\ {x}^{2}+{y}^{2}={\rho }^{2}&\end{array}\right.$转换为直角坐标方程为$x^{2}+(y-1)^{2}=1$,
因为$\dfrac{\pi }{4}\leqslant \theta \leqslant \dfrac{\pi }{2}$,$\dfrac{\pi }{2}\leqslant 2\theta \leqslant \pi$,$x=\rho \cos \theta =2\sin \theta \cos \theta =\sin 2\theta \in [0$,$1]$,
$y=\rho \sin \theta =2\sin ^{2}\theta =1-\cos 2\theta \in [1$,$2]$,
所以$C_{1}$的直角坐标方程为$x^{2}+(y-1)^{2}=1$,$x\in [0$,$1]$,$y\in [1$,$2]$;
(2)由于曲线$C_{1}$的方程为$x^{2}+(y-1)^{2}=1$,$(0\leqslant x\leqslant 1,1\leqslant y\leqslant 2)$,曲线$C_{2}:\left\{\begin{array}{l}{x=2\cos \alpha }\\ {y=2\sin \alpha }\end{array}\right.(\alpha$为参数,$\dfrac{\pi }{2} < \alpha < \pi )$,转换为直角坐标方程为$x^{2}+y^{2}=4$,$(-2 < x < 0,0 < y < 2)$;
如图所示:
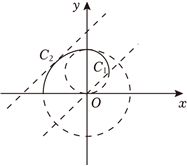
由于$y=x$与圆$C_{1}$相交于点$(1,1)$,即$m=0$,
当$m < 0$时,直线$y=x+m$与曲线$C_{1}$没有公共点;
当曲线$C_{2}$与直线$y=x+m$相切时,圆心$C_{2}(0,0)$到直线$y=x+m$的距离$d=\dfrac{\vert m\vert }{\sqrt{2}}=2$,解得$m=2\sqrt{2}$(负值舍去),
由于直线$y=x+m$与曲线$C_{2}$没有公共点,
所以$m > 2\sqrt{2}$,
故直线$y=x+m$既与$C_{1}$没有公共点,也与$C_{2}$没有公共点、实数$m$的取值范围为$(-\infty ,0)\bigcup (2\sqrt{2},+\infty )$.
点评:本题考查的知识要点:参数方程、极坐标方程和直角坐标方程之间的转换,直线与圆的位置关系,点到直线的距离公式,主要考查学生的理解能力和计算能力,属于中档题.
2023年高考数学乙卷-理21<-->2023年高考数学乙卷-理23
全网搜索"2023年高考数学乙卷-理22"相关
|

