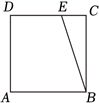
（5分）在正方形$ABCD$中，边长为1．$E$为线段$CD$的三等分点，$\overrightarrow{EC}=\dfrac{1}{2}\overrightarrow{DE}$，$\overrightarrow{BE}=\lambda \overrightarrow{BA}+\mu \overrightarrow{BC}$，则$\lambda +\mu =$____；若$F$为线段$BE$上的动点，$G$为$AF$中点，则$\overrightarrow{AF}\cdot \overrightarrow{DG}$的最小值为 ____．

答案：$\dfrac{4}{3}$；$-\dfrac{5}{18}$．
分析：由题意可知$\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DE}$，再结合$\overrightarrow{EC}=\dfrac{1}{2}\overrightarrow{DE}$可得$\overrightarrow{BE}=\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{BC}$，进而求出$\lambda$，$\mu$的值，得到$\lambda +\mu$的值；设$\overrightarrow{BF}=m\overrightarrow{BE}(0\leqslant m\leqslant 1)$，可得$\overrightarrow{AF}=(\dfrac{1}{3}m-1)\overrightarrow{BA}+m\overrightarrow{BC}$，$\overrightarrow{DG}=(\dfrac{1}{6}m-\dfrac{1}{2})\overrightarrow{BA}+(\dfrac{1}{2}m-1)\overrightarrow{BC}$，易知${\overrightarrow{BA}}^{2}=1$，$\overrightarrow{BA}\cdot \overrightarrow{BC}=0$，即可求出$\overrightarrow{AF}\cdot \overrightarrow{DG}$，再结合二次函数的性质求解即可．
解：由题意可知，$\overrightarrow{BE}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{BA}+\overrightarrow{BC}+\dfrac{2}{3}\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{BC}-\dfrac{2}{3}\overrightarrow{CD}=\overrightarrow{BA}+\overrightarrow{BC}-\dfrac{2}{3}\overrightarrow{BA}=\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{BC}$，
$\therefore$$\lambda =\dfrac{1}{3}$，$\mu =1$，
$\therefore \lambda +\mu =\dfrac{4}{3}$，
如图：

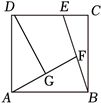
设$\overrightarrow{BF}=m\overrightarrow{BE}(0\leqslant m\leqslant 1)$，
则$\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}=-\overrightarrow{BA}+m\overrightarrow{BE}=-\overrightarrow{BA}+m(\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{BC})=(\dfrac{1}{3}m-1)\overrightarrow{BA}+m\overrightarrow{BC}$，
$\because G$为$AF$中点，
$\therefore$$\overrightarrow{DG}=\overrightarrow{DA}+\overrightarrow{AG}=-\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{AF}=-\overrightarrow{BC}+\dfrac{1}{2}[(\dfrac{1}{3}m-1)\overrightarrow{BA}+m\overrightarrow{BC}]=(\dfrac{1}{6}m-\dfrac{1}{2})\overrightarrow{BA}+(\dfrac{1}{2}m-1)\overrightarrow{BC}$，
$\because$正方形$ABCD$的边长为1，
$\therefore$${\overrightarrow{BA}}^{2}=1$，$\overrightarrow{BA}\cdot \overrightarrow{BC}=0$，
$\therefore$$\overrightarrow{AF}\cdot \overrightarrow{DG}=[(\dfrac{1}{3}m-1)\overrightarrow{BA}+m\overrightarrow{BC}]\cdot [(\dfrac{1}{6}m-\dfrac{1}{2})\overrightarrow{BA}+(\dfrac{1}{2}m-1)\overrightarrow{BC}]=(\dfrac{1}{3}m-1)(\dfrac{1}{6}m-\dfrac{1}{2})+m(\dfrac{1}{2}m-1)=\dfrac{5}{9}{m}^{2}-\dfrac{4}{3}m+\dfrac{1}{2}$，
对于函数$y=\dfrac{5}{9}{m}^{2}-\dfrac{4}{3}m+\dfrac{1}{2}$，对称轴为$m=\dfrac{6}{5}$，
$\therefore$函数$y=\dfrac{5}{9}{m}^{2}-\dfrac{4}{3}m+\dfrac{1}{2}$在$[0$，$1]$上单调递减，
$\therefore$当$m=1$时，函数$y=\dfrac{5}{9}{m}^{2}-\dfrac{4}{3}m+\dfrac{1}{2}$取得最小值$-\dfrac{5}{18}$，
即$\overrightarrow{AF}\cdot \overrightarrow{DG}$的最小为$-\dfrac{5}{18}$．
故答案为：$\dfrac{4}{3}$；$-\dfrac{5}{18}$．
点评：本题主要考查了平面向量的线性运算和数量积运算，考查了二次函数的性质，属于中档题．