（5分）双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a > 0,b > 0)$的左、右焦点分别为$F_{1}$、$F_{2}$．$P$是双曲线右支上一点，且直线$PF_{2}$的斜率为2，△$PF_{1}F_{2}$是面积为8的直角三角形，则双曲线的方程为$($　　$)$
A．$\dfrac{x^2}{2}-\dfrac{y^2}{8}=1$              B．$\dfrac{x^2}{4}-\dfrac{y^2}{8}=1$              C．$\dfrac{x^2}{8}-\dfrac{y^2}{2}=1$              D．$\dfrac{x^2}{8}-\dfrac{y^2}{4}=1$
答案：$A$
分析：设$\vert PF_{1}\vert =m$，$\vert PF_{2}\vert =n$，则$m-n=2a$，由△$PF_{1}F_{2}$是面积为8的直角三角形，可得$m^{2}+n^{2}=(2c)^{2}$，$\dfrac{1}{2}mn=8$，由直线$PF_{2}$的斜率为2，可得$\tan  \angle F_{1}F_{2}P=\dfrac{m}{n}=2$，即$m=2n$，从而求出$m$，$n$的值，进而求出$a$，$b$的值，得到双曲线的方程．
解：根据题意，画出图形，如下图：

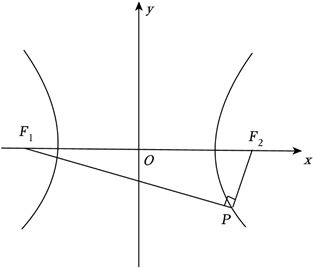
设$\vert PF_{1}\vert =m$，$\vert PF_{2}\vert =n$，
则$m-n=2a$，
因为△$PF_{1}F_{2}$是面积为8的直角三角形，
所以$m^{2}+n^{2}=(2c)^{2}=4c^{2}$，$\dfrac{1}{2}mn=8$，
因为直线$PF_{2}$的斜率为2，所以$\tan  \angle F_{1}F_{2}P=\dfrac{m}{n}=2$，
所以$m=2n$，
联立$\left\{\begin{array}{l}{m=2n}\\ {\dfrac{1}{2}mn=8}\end{array}\right.$，解得$\left\{\begin{array}{l}{m=4\sqrt{2}}\\ {n=2\sqrt{2}}\end{array}\right.$，
所以$2a=m-n=2\sqrt{2}$，即$a=\sqrt{2}$，
所以$4c^{2}=m^{2}+n^{2}=40$，即$c^{2}=10$，
所以$b^{2}=c^{2}-a^{2}=10-2=8$，
所以双曲线的方程为$\dfrac{{x}^{2}}{2}-\dfrac{{y}^{2}}{8}=1$．
故选：$A$．
点评：本题主要考查了双曲线的标准方程，考查了双曲线的性质，属于中档题．