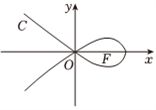
（6分）造型$\propto$可以做成美丽的丝带，将其看作图中的曲线$C$的一部分，已知$C$过坐标原点$O$，且$C$上的点满足横坐标大于$-2$，到点$F(2,0)$的距离与到定直线$x=a(a < 0)$的距离之积为4，则(　　)

A．$a=-2$              
B．点$(2\sqrt{2}$，$0)$在$C$上              
C．$C$在第一象限的纵坐标的最大值为1              
D．当点$(x_{0}$，$y_{0})$在$C$上时，$y_{0}\leqslant \dfrac{4}{{x}_{0}+2}$
答案：$ABD$
分析：结合题中新定义的曲线的性质对选项一一判断即可．
解：$A$对，因为$O$在曲线上，所以$O$到$x=a$的距离为$-a$，而$OF=2$，所以有$-a\cdot 2=4$，$a=-2$，那么曲线的方程为$(x+2)\sqrt{(x-2)^2+y^2}=4$，
$B$对，因为代入$(2\sqrt{2},0)$知满足方程；
$C$错，因为$y^2=(\dfrac{4}{x+2})^2-(x-2)^2=f(x)$，求导得$f'(x)=-\dfrac{32}{(x+2)^3}-2(x-2)$，那么有$f$（2）$=1$，$f'(2)=-\dfrac{1}{2} < 0$，
于是在$x=2$的左侧必存在一小区间$(2-s$，$2)(s$可以取无限小的数）上满足$f(x) > 1$，因此最大值一定大于1；
$D$对，曲线的方程为$(x+2)\sqrt{(x-2)^2+y^2}=4$，
可化为$(x-2)^{2}+y^{2}=(\frac{4}{x+2})^{2}$，
即$y^{2}=(\dfrac{4}{x+2})^{2}-(x-2)^{2}$，
因为$y_{0}^{2}=(\dfrac{4}{x_{0}+2})^{2}-(x_{0}-2)^{2}\leqslant (\dfrac{4}{x_{0}+2})^{2}\Rightarrow y_{0}\leqslant \dfrac{4}{x_{0}+2}$．
故选：$ABD$．
点评：本题考查了点的轨迹方程，新定义问题，是中档题．