（5分）在$\Delta ABC$中，$\angle BAC=60^\circ$，$AB=2$，$BC=\sqrt{6}$，$D$为$BC$上一点，$AD$为$\angle BAC$的平分线，则$AD=$____．
答案：2．
分析：在$\Delta ABC$中，根据正弦定理可求出$\angle ACB=45^\circ$，从而可得$\angle ABC=\angle ADB=75^\circ$，即得$AD=AB=2$．
解：

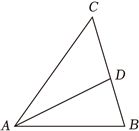
如图，$\because$在$\Delta ABC$中，$AB=2$，$\angle BAC=60^\circ ,BC=\sqrt{6}$，
$\therefore$由正弦定理可得$\dfrac{BC}{\sin \angle BAC}=\dfrac{AB}{\sin \angle ACB}$，
$\therefore \sin \angle ACB=\dfrac{AB\times \sin \angle BAC}{BC}=\dfrac{2\times \dfrac{\sqrt{3}}{2}}{\sqrt{6}}=\dfrac{\sqrt{2}}{2}$，又$\angle BAC=60^\circ$，
$\therefore \angle ACB=45^\circ$，$\therefore \angle ABC=180^\circ -45^\circ -60^\circ =75^\circ$，
又$AD$为$\angle BAC$的平分线，且$\angle BAC=60^\circ$，
$\therefore \angle BAD=30^\circ$，又$\angle ABC=75^\circ$，$\therefore \angle ADB=75^\circ$，
$\therefore AD=AB=2$．
故答案为：2．

点评：本题考查解三角形问题，正弦定理的应用，属中档题．