（5分）在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$E$，$F$分别为$CD$，$A_{1}B_{1}$的中点，则以$EF$为直径的球面与正方体每条棱的交点总数为 ____．
答案：12．
分析：根据正方体的对称性，可知球心到各棱距离相等，由此能求出结果．
解：在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$E$，$F$分别为$CD$，$A_{1}B_{1}$的中点，
设正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中棱长为2，$EF$中点为$O$，
取$AB$，$BB_{1}$中点$G$，$M$，侧面$BB_{1}C_{1}C$的中心为$N$，
连接$FG$，$EG$，$OM$，$ON$，$MN$，如图，

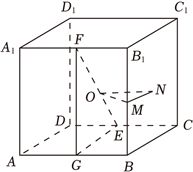
由题意得$O$为球心，在正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$EF=\sqrt{F{G}^{2}+E{G}^{2}}=\sqrt{4+4}=2\sqrt{2}$，
$\therefore R=\sqrt{2}$，
则球心$O$到$BB_{1}$的距离为$OM=\sqrt{O{N}^{2}+M{N}^{2}}=\sqrt{1+1}=\sqrt{2}$，
$\therefore$球$O$与棱$BB_{1}$相切，球面与棱$BB_{1}$只有一个交点，
同理，根据正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$的对称性可知，其余各棱和球面也只有一个交点，
$\therefore$以$EF$为直径的球面与正方体每条棱的交点总数为12．
故答案为：12．
点评：本题考查正方体的对称性、球心到各棱距离等基础知识，考查运算求解能力，是中档题．