（10分）记$\Delta ABC$的内角$A$，$B$，$C$的对边分别为$a$，$b$，$c$，已知$\Delta ABC$面积为$\sqrt{3}$，$D$为$BC$的中点，且$AD=1$．
（1）若$\angle ADC=\dfrac{\pi }{3}$，求$\tan B$；
（2）若$b^{2}+c^{2}=8$，求$b$，$c$．
分析：（1）根据已知条件，推得$S_{\Delta ACD}=\dfrac{\sqrt{3}}{2}$，过$A$作$AE\bot BC$，垂足为$E$，依次求出$AE$，$BE$，即可求解；
（2）根据已知条件，求得$\overrightarrow{AD}=\dfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$，两边同时平方，再结合三角形的面积公式，即可求解．
解：（1）$)D$为$BC$中点，$S_{\Delta ABC}=\sqrt{3}$，
则$S_{\Delta ACD}=\dfrac{\sqrt{3}}{2}$，
过$A$作$AE\bot BC$，垂足为$E$，如图所示：

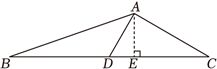
$\Delta ADE$中，$DE=\dfrac{1}{2}$，$AE=\dfrac{\sqrt{3}}{2}$，$S_{\Delta ACD}=\dfrac{1}{2}\cdot \dfrac{\sqrt{3}}{2}CD=\dfrac{\sqrt{3}}{2}$，解得$CD=2$，
$\therefore BD=2$，$BE=\dfrac{5}{2}$，
故$\tan B=\dfrac{AE}{BE}=\dfrac{\dfrac{\sqrt{3}}{2}}{\dfrac{5}{2}}=\dfrac{\sqrt{3}}{5}$；
（2）$\overrightarrow{AD}=\dfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$，
$\overrightarrow{AD}^2=\dfrac{1}{4}(c^2+b^2+2bc\cos A)$，
$AD=1$，$b^{2}+c^{2}=8$，
则$1=\dfrac{1}{4}(8+2bc\cos A)$，
$\therefore bc\cos A=-2$①，
${{S}_{\Delta ABC}}=\dfrac{1}{2}bc\sin A=\sqrt{3}$，即$bc\sin A=2\sqrt{3}$②，
由①②解得$\tan A=-\sqrt{3}$，
$\therefore$$A=\dfrac{2\pi }{3}$，
$\therefore bc=4$，又$b^{2}+c^{2}=8$，
$\therefore b=c=2$．
点评：本题主要考查三角形中的几何计算，考查转化能力，属于中档题．