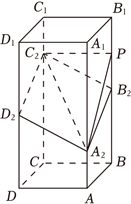
（12分）如图，在正四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$AB=2$，$AA_{1}=4$．点$A_{2}$，$B_{2}$，$C_{2}$，$D_{2}$分别在棱$AA_{1}$，$BB_{1}$，$CC_{1}$，$DD_{1}$上，$AA_{2}=1$，$BB_{2}=DD_{2}=2$，$CC_{2}=3$．
（1）证明：$B_{2}C_{2}//A_{2}D_{2}$；
（2）点$P$在棱$BB_{1}$上，当二面角$P-A_{2}C_{2}-D_{2}$为$150^\circ$时，求$B_{2}P$．

分析：（1）建系，根据坐标法及向量共线定理，即可证明；
（2）建系，根据向量法，向量夹角公式，方程思想，即可求解．
解：

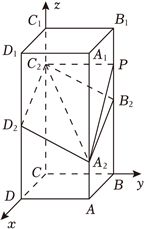
（1）证明：根据题意建系如图，则有：
$B_{2}(0$，2，$2)$，$C_{2}(0$，0，$3)$，$A_{2}(2$，2，$1)$，$D_{2}(2$，0，$2)$，
$\therefore$$\overrightarrow{{B}_{2}{C}_{2}}=(0,-2,1)$，$\overrightarrow{{A}_{2}{D}_{2}}=(0,-2,1)$，
$\therefore$$\overrightarrow{{B}_{2}{C}_{2}}=\overrightarrow{{A}_{2}{D}_{2}}$，又$B_{2}$，$C_{2}$，$A_{2}$，$D_{2}$四点不共线，
$\therefore B_{2}C_{2}//A_{2}D_{2}$；
（2）在（1）的坐标系下，可设$P(0$，2，$t)$，$t\in [0$，$4]$，
又由（1）知$C_{2}(0$，0，$3)$，$A_{2}(2$，2，$1)$，$D_{2}(2$，0，$2)$，
$\therefore$$\overrightarrow{{C}_{2}{A}_{2}}=(2,2,-2)$，$\overrightarrow{{C}_{2}P}=(0,2,t-3)$，$\overrightarrow{{A}_{2}{D}_{2}}=(0,-2,1)$，
设平面$PA_{2}C_{2}$的法向量为$\overrightarrow{m}=(x,y,z)$，
则$\left\{\begin{array}{l}{\overrightarrow{m}\cdot \overrightarrow{{C}_{2}{A}_{2}}=2x+2y-2z=0}\\ {\overrightarrow{m}\cdot \overrightarrow{{C}_{2}P}=2y+(t-3)z=0}\end{array}\right.$，取$\overrightarrow{m}=(t-1,3-t,2)$，
设平面$A_{2}C_{2}D_{2}$的法向量为$\overrightarrow{n}=(a,b,c)$，
则$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{{C}_{2}{A}_{2}}=2a+2b-2c=0}\\ {\overrightarrow{n}\cdot \overrightarrow{{A}_{2}{D}_{2}}=-2b+c=0}\end{array}\right.$，取$\overrightarrow{n}=(1,1,2)$，
$\therefore$根据题意可得$\vert \cos 150^\circ \vert =\vert \cos  < \overrightarrow{m}$，$\overrightarrow{n} > \vert =\dfrac{\vert \overrightarrow{m}\cdot \overrightarrow{n}\vert }{\vert \overrightarrow{m}\vert \vert \overrightarrow{n}\vert }$，
$\therefore$$\dfrac{\sqrt{3}}{2}=\dfrac{6}{\sqrt{(t-1)^{2}+(3-t)^{2}+4}\times \sqrt{6}}$，
$\therefore t^{2}-4t+3=0$，又$t\in [0$，$4]$，
$\therefore$解得$t=1$或$t=3$，
$\therefore P$为$B_{1}B_{2}$的中点或$B_{2}B$的中点，
$\therefore B_{2}P=1$．
点评：本题考查利用向量法证明线线平行，利用向量法求解二面角问题，向量共线定理及向量夹角公式的应用，方程思想，属中档题．