（5分）在正四棱台$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$AB=2$，$A_{1}B_{1}=1$，$AA_{1}=\sqrt{2}$，则该棱台的体积为 　$\dfrac{7\sqrt{6}}{6}$　．
分析：先根据题意求出四棱台的高，再代入台体的体积公式即可求解．
解：

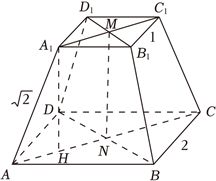
如图，设正四棱台$ABCD-A_{1}B_{1}C_{1}D_{1}$的上下底面中心分别为$M$，$N$，
过$A_{1}$作$A_{1}H\bot AC$，垂足点为$H$，由题意易知$A_{1}M=HN=\dfrac{\sqrt{2}}{2}$，又$AN=\sqrt{2}$，
$\therefore AH=AN-HN=\dfrac{\sqrt{2}}{2}$，又$AA_{1}=\sqrt{2}$，$\therefore A_{1}H=MN=\dfrac{\sqrt{6}}{2}$，
$\therefore$该四棱台的体积为$\dfrac{1}{3}\times (1+4+\sqrt{1\times 4})\times \dfrac{\sqrt{6}}{2}=\dfrac{7\sqrt{6}}{6}$．
故答案为：$\dfrac{7\sqrt{6}}{6}$．
点评：本题考查台体的体积公式的应用，属基础题．