（5分）下列物体中，能够被整体放入棱长为1（单位：$m)$的正方体容器（容器壁厚度忽略不计）内的有$($　　$)$
A．直径为$0.99m$的球体              
B．所有棱长均为$1.4m$的四面体              
C．底面直径为$0.01m$，高为$1.8m$的圆柱体              
D．底面直径为$1.2m$，高为$0.01m$的圆柱体
答案：$ABD$
分析：对于$A$，由正方体的内切球直径大于0.99可判断；对于$B$，由正方体内部最大的正四面体的棱长大于1.4可判断；对于$C$，由正方体的体对角线小于1.8可判断；对于$D$，取$E$，$F$，$G$，$H$，$I$，$J$都为棱中点，则六边形$EFGHIJ$为正六边形，由正六边形的内切圆直径大于1.2可判断．
解：对于$A$，棱长为1的正方体内切球的直径为$1 > 0.99$，选项$A$正确；
对于$B$，如图，

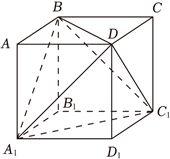
正方体内部最大的正四面体$D-A_{1}BC_{1}$的棱长为$\sqrt{{1}^{2}+{1}^{2}}=\sqrt{2} > 1.4$，选项$B$正确；
对于$C$，棱长为1的正方体的体对角线为$\sqrt{3} < 1.8$，选项$C$错误；
对于$D$，如图，六边形$EFGHIJ$为正六边形，$E$，$F$，$G$，$H$，$I$，$J$为棱的中点，

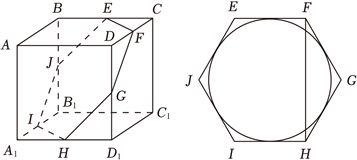
高为0.01米可忽略不计，看作直径为1.2米的平面圆，
六边形$EFGHIJ$棱长为$\dfrac{\sqrt{2}}{2}$米，$\angle GFH=\angle GHF=30^\circ$，
所以$FH=\sqrt{3}FG=\sqrt{3}GH=\dfrac{\sqrt{6}}{2}$米，故六边形$EFGHIJ$内切圆直径为$\dfrac{\sqrt{6}}{2}$米，
而$(\dfrac{\sqrt{6}}{2})^{2}=\dfrac{3}{2} > (1.2)^{2}=1.44$，选项$D$正确．
故选：$ABD$．
点评：本题考查简单几何体的体积，考查空间想象能力与运算求解能力，属于中档题．