（5分）如图，四边形$ABCD$为正方形，$ED\bot$平面$ABCD$，$FB//ED$，$AB=ED=2FB$．记三棱锥$E-ACD$，$F-ABC$，$F-ACE$的体积分别为$V_{1}$，$V_{2}$，$V_{3}$，则(　　)

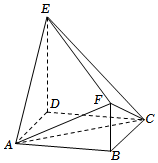
A．$V_{3}=2V_{2}$              B．$V_{3}=V_{1}$              C．$V_{3}=V_{1}+V_{2}$              D．$2V_{3}=3V_{1}$
分析：利用直接法与等体积法直接计算各三棱锥的体积，进而可得$V_{1}$、$V_{2}$、$V_{3}$之间的关系．
解：设$AB=ED=2FB=2$，
$V_{1}=\dfrac{1}{3}\times S_{\Delta ACD}\times \vert ED\vert =\dfrac{4}{3}$，
$V_{2}=\dfrac{1}{3}\times S_{\Delta ABC}\times \vert FB\vert =\dfrac{2}{3}$，
如图所示，

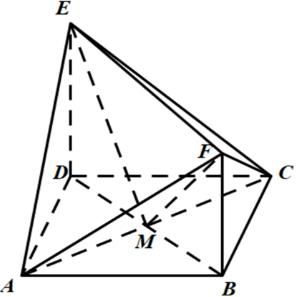
连接$BD$交$AC$于点$M$，连接$EM$、$FM$，
则$FM=\sqrt{3}$，$EM=\sqrt{6}$，$EF=3$，
故$S_{\Delta EMF}=\dfrac{1}{2}\times \sqrt{3}\times \sqrt{6}=\dfrac{3\sqrt{2}}{2}$，
$V_{3}=\dfrac{1}{3}S_{\Delta EMF}\times AC=\dfrac{1}{3}\times \dfrac{3\sqrt{2}}{2}\times 2\sqrt{2}=2$，
故$C$、$D$正确，$A$、$B$错误．
故选：$CD$．
点评：本题主要考查组合体的体积，熟练掌握棱锥的体积公式是解决本题的关键．