（5分）已知函数$f(x)=\sin (2x+\varphi )(0 < \varphi  < \pi )$的图像关于点$(\dfrac{2\pi }{3}$，$0)$中心对称，则(　　)
A．$f(x)$在区间$(0,\dfrac{5\pi }{12})$单调递减              
B．$f(x)$在区间$(-\dfrac{\pi }{12}$，$\dfrac{11\pi }{12})$有两个极值点              
C．直线$x=\dfrac{7\pi }{6}$是曲线$y=f(x)$的对称轴              
D．直线$y=\dfrac{\sqrt{3}}{2}-x$是曲线$y=f(x)$的切线
分析：直接利用函数的对称性求出函数的关系式，进一步利用函数的性质的判断$A$、$B$、$C$、$D$的真假．
解：因为$f(x)=\sin (2x+\varphi )(0 < \varphi  < \pi )$的图象关于点$(\dfrac{2\pi }{3}$，$0)$对称，
所以$2\times \dfrac{2\pi }{3}+\varphi =k\pi$，$k\in Z$，
所以$\varphi =k\pi -\dfrac{4\pi }{3}$，
因为$0 < \varphi  < \pi$，
所以$\varphi =\dfrac{2\pi }{3}$，
故$f(x)=\sin (2x+\dfrac{2\pi }{3})$，
令$\dfrac{\pi }{2} < 2x+\dfrac{2\pi }{3} < \dfrac{3\pi }{2}$，解得$-\dfrac{\pi }{12} < x < \dfrac{5\pi }{12}$，
故$f(x)$在$(0,\dfrac{5\pi }{12})$单调递减，$A$正确；
$x\in (-\dfrac{\pi }{12}$，$\dfrac{11\pi }{12})$，$2x+\dfrac{2\pi }{3}\in (\dfrac{\pi }{2}$，$\dfrac{5\pi }{2})$，
根据函数的单调性，故函数$f(x)$在区间$(-\dfrac{\pi }{12}$，$\dfrac{11\pi }{12})$只有一个极值点，故$B$错误；
令$2x+\dfrac{2\pi }{3}=k\pi +\dfrac{\pi }{2}$，$k\in Z$，得$x=\dfrac{k\pi }{2}-\dfrac{\pi }{12}$，$k\in Z$，$C$显然错误；
结合正弦函数的图象可知，

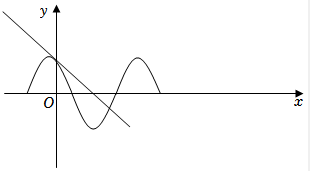
直线$y=\dfrac{\sqrt{3}}{2}-x$显然与$y=\sin (2x+\dfrac{2\pi }{3})$相切，故直线$y=\dfrac{\sqrt{3}}{2}-x$显然是曲线的切线，故$D$正确．
故选：$AD$．
点评：本题考查的知识要点：三角函数关系式的求法，函数的性质的应用，主要考查学生的运算能力和数学思维能力，属于基础题．