（5分）已知正三棱台的高为1，上、下底面边长分别为$3\sqrt{3}$和$4\sqrt{3}$，其顶点都在同一球面上，则该球的表面积为(　　)
A．$100\pi$              B．$128\pi$              C．$144\pi$              D．$192\pi$
分析：求出上底面及下底面所在平面截球所得圆的半径，作出轴截面图，根据几何知识可求得球的半径，进而得到其表面积．
解：当球心在台体外时，由题意得，上底面所在平面截球所得圆的半径为$\dfrac{3\sqrt{3}}{2\sin 60^\circ }=3$，下底面所在平面截球所得圆的半径为$\dfrac{4\sqrt{3}}{2\sin 60^\circ }=4$，如图，

设球的半径为$R$，则轴截面中由几何知识可得$\sqrt{{R}^{2}-{3}^{2}}-\sqrt{{R}^{2}-{4}^{2}}=1$，解得$R=5$，
$\therefore$该球的表面积为$4\pi R^{2}=4\pi \times 25=100\pi$．
当球心在台体内时，如图，

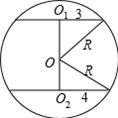
此时$\sqrt{{R}^{2}-{3}^{2}}+\sqrt{{R}^{2}-{4}^{2}}=1$，无解．
综上，该球的表面积为$100\pi$．
故选：$A$．
点评：本题考查球的表面积求解，同时还涉及了正弦定理的运用，考查了运算求解能力，对空间想象能力要求较高，属于较难题目．