（5分）已知正四棱锥的侧棱长为$l$，其各顶点都在同一球面上．若该球的体积为$36\pi$，且$3\leqslant l\leqslant 3\sqrt{3}$，则该正四棱锥体积的取值范围是(　　)
A．$[18$，$\dfrac{81}{4}]$              B．$[\dfrac{27}{4}$，$\dfrac{81}{4}]$              C．$[\dfrac{27}{4}$，$\dfrac{64}{3}]$              D．$[18$，$27]$
分析：画出图形，由题意可知求出球的半径$R=3$，设正四棱锥的底面边长为$a$，高为$h$，由勾股定理可得${l}^{2}=\dfrac{1}{2}{a}^{2}+{h}^{2}$，又${R}^{2}=(h-3)^{2}+(\dfrac{\sqrt{2}a}{2})^{2}$，所以$l^{2}=6h$，由$l$的取值范围求出$h$的取值范围，又因为$a^{2}=12h-2h^{2}$，所以该正四棱锥体积$V(h)=-\dfrac{2}{3}{h}^{3}+4{h}^{2}$，利用导数即可求出$V(h)$的取值范围．
解：

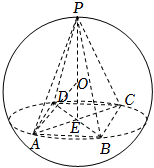
如图所示，正四棱锥$P-ABCD$各顶点都在同一球面上，连接$AC$与$BD$交于点$E$，连接$PE$，则球心$O$在直线$PE$上，连接$OA$，
设正四棱锥的底面边长为$a$，高为$h$，
在$\rm{Rt}\Delta PAE$中，$PA^{2}=AE^{2}+PE^{2}$，即${l}^{2}=(\dfrac{\sqrt{2}a}{2})^{2}+{h}^{2}=\dfrac{1}{2}{a}^{2}+{h}^{2}$，
$\because$球$O$的体积为$36\pi$，$\therefore$球$O$的半径$R=3$，
在$\rm{Rt}\Delta OAE$中，$OA^{2}=OE^{2}+AE^{2}$，即${R}^{2}=(h-3)^{2}+(\dfrac{\sqrt{2}a}{2})^{2}$，
$\therefore$$\dfrac{1}{2}{a}^{2}+{h}^{2}-6h=0$，$\therefore$$\dfrac{1}{2}{a}^{2}+{h}^{2}=6h$，
$\therefore l^{2}=6h$，又$\because 3\leqslant l\leqslant 3\sqrt{3}$，$\therefore$$\dfrac{3}{2}\leqslant h\leqslant \dfrac{9}{2}$，
$\therefore$该正四棱锥体积$V(h)=\dfrac{1}{3}{a}^{2}h=\dfrac{1}{3}(12h-2{h}^{2})h=-\dfrac{2}{3}{h}^{3}+4{h}^{2}$，
$\because V'(h)=-2h^{2}+8h=2h(4-h)$，
$\therefore$当$\dfrac{3}{2}\leqslant h < 4$时，$V'(h) > 0$，$V(h)$单调递增；当$4 < h\leqslant \dfrac{9}{2}$时，$V'(h) < 0$，$V(h)$单调递减，
$\therefore V(h)_{max}=V$（4）$=\dfrac{64}{3}$，
又$\because V(\dfrac{3}{2})=\dfrac{27}{4}$，$V(\dfrac{9}{2})=\dfrac{81}{4}$，且$\dfrac{27}{4} < \dfrac{81}{4}$，
$\therefore$$\dfrac{27}{4}\leqslant V(h)\leqslant \dfrac{64}{3}$，
即该正四棱锥体积的取值范围是$[\dfrac{27}{4}$，$\dfrac{64}{3}]$，
故选：$C$．

点评：本题主要考查了正四棱锥的外接球问题，考查了利用导数研究函数的最值，属于中档题．