（5分）在$\Delta ABC$中，点$D$在边$AB$上，$BD=2DA$．记$\overrightarrow{CA}=\overrightarrow{m}$，$\overrightarrow{CD}=\overrightarrow{n}$，则$\overrightarrow{CB}=($　　)
A．$3\overrightarrow{m}-2\overrightarrow{n}$              B．$-2\overrightarrow{m}+3\overrightarrow{n}$              C．$3\overrightarrow{m}+2\overrightarrow{n}$              D．$2\overrightarrow{m}+3\overrightarrow{n}$
分析：直接利用平面向量的线性运算可得$\dfrac{1}{2}\overrightarrow{CB}=\dfrac{3}{2}\overrightarrow{CD}-\overrightarrow{CA}$，进而得解．
解：如图，

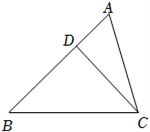
$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}=\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{DB}=\overrightarrow{CA}+\dfrac{1}{2}(\overrightarrow{CB}-\overrightarrow{CD})=\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}-\dfrac{1}{2}\overrightarrow{CD}$，
$\therefore$$\dfrac{1}{2}\overrightarrow{CB}=\dfrac{3}{2}\overrightarrow{CD}-\overrightarrow{CA}$，即$\overrightarrow{CB}=3\overrightarrow{CD}-2\overrightarrow{CA}=3\overrightarrow{n}-2\overrightarrow{m}$．
故选：$B$．
点评：本题主要考查平面向量的线性运算，考查运算求解能力，属于基础题．