21．（12分）已知$a>0$且$a\ne 1$，函数$f(x)=\dfrac{{x}^{a}}{{a}^{x}}$$(x>0)$．
（1）当$a=2$时，求$f(x)$的单调区间；
（2）若曲线$y=f(x)$与直线$y=1$有且仅有两个交点，求$a$的取值范围．
分析：（1）求出$a=2$时$f(x)$的解析式，求导，利用导数与单调性的关系即可求解；
（2）将已知转化为$f(x)=1$在$(0,+\infty )$有两个不等实根，变形可得$\dfrac{lnx}{x}=\dfrac{lna}{a}$，令$g(x)=\dfrac{lnx}{x}$，利用导数求出$g(x)$的单调性及$g(x)$的大致图象，即可求解$a$的取值范围．
解：（1）$a=2$时，$f(x)=\dfrac{{x}^{2}}{{2}^{x}}$，
$f\prime (x)=\dfrac{2x\cdot {2}^{x}-{2}^{x}ln2\cdot {x}^{2}}{({2}^{x})^{2}}=\dfrac{x(2-xln2)}{{2}^{x}}=\dfrac{ln2\cdot x(\dfrac{2}{ln2}-x)}{{2}^{x}}$，
当$x\in (0,\dfrac{2}{ln2})$时，$f\prime (x)>0$，当$x\in (\dfrac{2}{ln2}$，$+\infty )$时，$f\prime (x)<0$，
故$f(x)$在$(0,\dfrac{2}{ln2})$上单调递增，在$(\dfrac{2}{ln2}$，$+\infty )$上单调递减．
（2）由题知$f(x)=1$在$(0,+\infty )$有两个不等实根，
$f(x)=1\Harr x^{a}=a^{x}\Harr alnx=xlna\Harr \dfrac{lnx}{x}=\dfrac{lna}{a}$，
令$g(x)=\dfrac{lnx}{x}$，$g\prime (x)=\dfrac{1-lnx}{{x}^{2}}$，$g(x)$在$(0,e)$上单调递增，在$(e,+\infty )$上单调递减，
又$\lim\limits_{x\rarr 0}g(x)=-\infty$，$g$（e）$=\dfrac{1}{e}$，$g$（1）$=0$，$\lim\limits_{x\rarr +\infty }g(x)=0$，
作出$g(x)$的图象，如图所示：

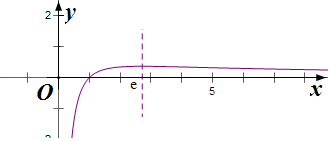
由图象可得$0<\dfrac{lna}{a}<\dfrac{1}{e}$，解得$a>1$且$a\ne e$，
即$a$的取值范围是$(1$，$e)\bigcup (e$，$+\infty )$．

点评：本题主要考查利用导数研究函数的单调性，考查转化思想与运算求解能力，属于中档题．