|
19．（12分）在四棱锥Q−ABCD中，底面ABCD是正方形，若AD=2，QD=QA=√5，QC=3．
（Ⅰ）求证：平面QAD⊥平面ABCD；
（Ⅱ）求二面角B−QD−A的平面角的余弦值．
分析：（Ⅰ）由CD2+QD2=QC2证明CD⊥QD，再由CD⊥AD，证明CD⊥平面QAD，即可证明平面QAD⊥平面ABCD．
（Ⅱ）取AD的中点O，在平面ABCD内作Ox⊥AD，以OD为y轴，OQ为z轴，建立空间直角坐标系，求出平面ADQ的一个法向量→α，平面BDQ的一个法向量→β，再求cos<→α，→β>即可．
（Ⅰ）证明：ΔQCD中，CD=AD=2，QD=√5，QC=3，所以CD2+QD2=QC2，所以CD⊥QD；
又CD⊥AD，AD⋂QD=D，AD\sub平面QAD，QD\sub平面QAD，所以CD⊥平面QAD；
又CD\sub平面ABCD，所以平面QAD⊥平面ABCD．
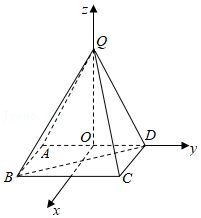
（Ⅱ）解：取AD的中点O，在平面ABCD内作Ox⊥AD，
以OD为y轴，OQ为z轴，建立空间直角坐标系O−xyz，如图所示：
则O(0，0，0)，B(2，−1，0)，D(0，1，0)，Q(0，0，2)，
因为Ox⊥平面ADQ，所以平面ADQ的一个法向量为→α=(1，0，0)，
设平面BDQ的一个法向量为→β=(x，y，z)，
由→BD=(−2，2，0)，→DQ=(0，−1，2)，
得{→β⋅→BD=0→β⋅→DQ=0，即{−2x+2y=0−y+2z=0，
令z=1，得y=2，x=2，所以→β=(2，2，1)；
所以cos<→α，→β>=→α⋅→β|→α|⋅|→β|=2+0+01×√4+4+1=23，
所以二面角B−QD−A的平面角的余弦值为23．
点评：本题考查了空间中的垂直关系应用问题，也考查了利用空间向量求二面角的余弦值应用问题，也可以直接利用二面角的定义求二面角的余弦值，是中档题．
|
