（12分）如图，在三棱锥$A-BCD$中，平面$ABD\bot$平面$BCD$，$AB=AD$，$O$为$BD$的中点．
（1）证明：$OA\bot CD$；
（2）若$\Delta OCD$是边长为1的等边三角形，点$E$在棱$AD$上，$DE=2EA$，且二面角$E-BC-D$的大小为$45^\circ$，求三棱锥$A-BCD$的体积．

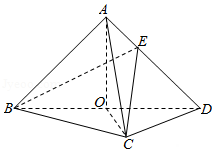
分析：（1）利用等腰三角形中线就是高，得到$AO\bot BD$，然后利用面面垂直的性质，得到$AO\bot$平面$BCD$，再利用线面垂直的性质，即可证明$AO\bot CD$；
（2）建立合适的空间直角坐标系，设$A(0$，0，$t)$，利用待定系数法求出平面的法向量，由向量的夹角公式求出$t$的值，然后利用锥体的体积公式求解即可．
解：（1）证明：因为$AB=AD$，$O$为$BD$的中点，所以$AO\bot BD$，
又平面$ABD\bot$平面$BCD$，平面$ABD\cap$平面$BCD=BD$，$AO\subset$平面$BCD$，
所以$AO\bot$平面$BCD$，又$CD\subset$平面$BCD$，
所以$AO\bot CD$；
（2）取$OD$的中点$F$，因为$\Delta OCD$为正三角形，所以$CF\bot OD$，
过$O$作$OM//CF$与$BC$交于点$M$，则$OM\bot OD$，
所以$OM$，$OD$，$OA$两两垂直，
以点$O$为坐标原点，分别以$OM$，$OD$，$OA$为$x$轴，$y$轴，$z$轴建立空间直角坐标系如图所示，



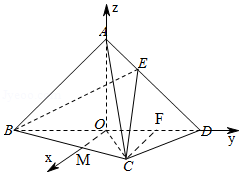
则$B(0$，$-1$，$0)$，$C(\dfrac{\sqrt{3}}{2},\dfrac{1}{2},0)$，$D(0$，1，$0)$，
设$A(0$，0，$t)$，则$E(0,\dfrac{1}{3},\dfrac{2t}{3})$，
因为$OA\bot$平面$BCD$，故平面$BCD$的一个法向量为$\overrightarrow{OA}=(0,0,t)$，
设平面$BCE$的法向量为$\overrightarrow{n}=(x,y,z)$，
又$\overrightarrow{BC}=(\dfrac{\sqrt{3}}{2},\dfrac{3}{2},0),\overrightarrow{BE}=(0,\dfrac{4}{3},\dfrac{2t}{3})$，
所以由$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{BC}=0}\\ {\overrightarrow{n}\cdot \overrightarrow{BE}=0}\end{array}\right.$，得$\left\{\begin{array}{l}{\dfrac{\sqrt{3}}{2}x+\dfrac{3}{2}y=0}\\ {\dfrac{4}{3}y+\dfrac{2t}{3}z=0}\end{array}\right.$，
令$x=\sqrt{3}$，则$y=-1$，$z=\dfrac{2}{t}$，故$\overrightarrow{n}=(\sqrt{3},-1,\dfrac{2}{t})$，
因为二面角$E-BC-D$的大小为$45^\circ$，
所以$\vert \cos <\overrightarrow{n},\overrightarrow{OA}>\vert =\dfrac{\vert \overrightarrow{n}\cdot \overrightarrow{OA}\vert }{\vert \overrightarrow{n}\vert \vert \overrightarrow{OA}\vert }=\dfrac{2}{t\sqrt{4+\dfrac{4}{{t}^{2}}}}=\dfrac{\sqrt{2}}{2}$，
解得$t=1$，所以$OA=1$，
又${S}_{\Delta OCD}=\dfrac{1}{2}\times 1\times 1\times \dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{4}$，所以${S}_{\Delta BCD}=\dfrac{\sqrt{3}}{2}$，
故${V}_{A-BCD}=\dfrac{1}{3}\cdot {S}_{\Delta BCD}\cdot OA=\dfrac{1}{3}\times \dfrac{\sqrt{3}}{2}\times 1=\dfrac{\sqrt{3}}{6}$．

点评：本题考查了面面垂直和线面垂直的性质，在求解有关空间角问题的时候，一般要建立合适的空间直角坐标系，将空间角问题转化为空间向量问题，属于中档题．