（12分）如图，四棱锥$P-ABCD$的底面为正方形，$PD\bot$底面$ABCD$．设平面$PAD$与平面$PBC$的交线为$l$．

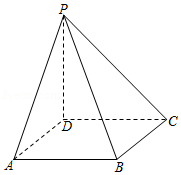
（1）证明：$l\bot$平面$PDC$；
（2）已知$PD=AD=1$，$Q$为$l$上的点，$QB=\sqrt{2}$，求$PB$与平面$QCD$所成角的正弦值．
分析：（1）过$P$在平面$PAD$内作直线$l//AD$，推得$l$为平面$PAD$和平面$PBC$的交线，由线面垂直的判定和性质，即可得证；
（2）以$D$为坐标原点，直线$DA$，$DC$，$DP$所在的直线为$x$，$y$，$z$轴，建立空间直角坐标系$D-xyz$，求出$Q(0$，1，$1)$，运用向量法，求得平面$QCD$的法向量，结合向量的夹角公式求解即可．
解答：（1）证明：过$P$在平面$PAD$内作直线$l//AD$，
由$AD//BC$，可得$l//BC$，即$l$为平面$PAD$和平面$PBC$的交线，
$\because PD\bot$平面$ABCD$，$BC\subset $平面$ABCD$，$\therefore PD\bot BC$，
又$BC\bot CD$，$CD\bigcap PD=D$，$\therefore BC\bot$平面$PCD$，
$\because l//BC$，$\therefore l\bot$平面$PCD$；
（2）解：如图，以$D$为坐标原点，直线$DA$，$DC$，$DP$所在的直线为$x$，$y$，$z$轴，建立空间直角坐标系$D-xyz$，
$\because PD=AD=1$，$Q$为$l$上的点，$QB=\sqrt{2}$，
$\therefore PB=\sqrt{3}$，$QP=1$，

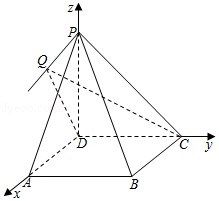
则$D(0$，0，$0)$，$A(1$，0，$0)$，$C(0$，1，$0)$，$P(0$，0，$1)$，$B(1$，1，$0)$，作$PQ//AD$，则$PQ$为平面$PAD$与平面$PBC$的交线为$l$，因为$QB=\sqrt{2}$，$\Delta QAB$是等腰直角三角形，所以$Q(1$，0，$1)$，
则$\overrightarrow{DQ}=(1$，0，$1)$，$\overrightarrow{PB}=(1$，1，$-1)$，$\overrightarrow{DC}=(0$，1，$0)$，
设平面$QCD$的法向量为$\overrightarrow{n}=(a$，$b$，$c)$，
则$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{DC}=0}\\ {\overrightarrow{n}\cdot \overrightarrow{DQ}=0}\end{array}\right.$，$\therefore$$\left\{\begin{array}{l}{b=0}\\ {a+c=0}\end{array}\right.$，取$c=1$，可得$\overrightarrow{n}=(-1$，0，$1)$，
$\therefore \cos <\overrightarrow{n}$，$\overrightarrow{PB}>=\dfrac{\overrightarrow{n}\cdot \overrightarrow{PB}}{\vert \overrightarrow{n}\vert \vert \overrightarrow{PB}\vert }=\dfrac{-1-1}{\sqrt{3}\cdot \sqrt{2}}=\dfrac{\sqrt{6}}{3}$，
$\therefore PB$与平面$QCD$所成角的正弦值为$\dfrac{\sqrt{6}}{3}$．
点评：本题考查空间线面垂直的判定，以及线面角的求法，考查转化思想和向量法的运用，考查运算能力和推理能力，属于中档题．