已知正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$的棱长为2，$M$、$N$分别为$BB_{1}$、$AB$的中点，则三棱锥$A-NMD_{1}$的体积为____．
分析：由题意画出图形，再由等体积法求三棱锥$A-NMD_{1}$的体积．
解答：如图，

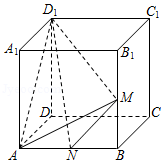
$\because$正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$的棱长为2，$M$、$N$分别为$BB_{1}$、$AB$的中点，
$\therefore$${S}_{\Delta ANM}=\dfrac{1}{2}\times 1\times 1=\dfrac{1}{2}$，
$\therefore$${V}_{A-NM{D}_{1}}={V}_{{D}_{1}-AMN}=\dfrac{1}{3}\times \dfrac{1}{2}\times 2=\dfrac{1}{3}$．
故答案为：$\dfrac{1}{3}$．
点评：本题考查利用等体积法求多面体的体积，是基础的计算题．