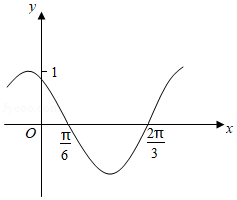
如图是函数$y=\sin (\omega x+\varphi )$的部分图象，则$\sin (\omega x+\varphi )=$(　　)

A．$\sin (x+\dfrac{\pi }{3})$              
B．$\sin (\dfrac{\pi }{3}-2x)$              
C．$\cos (2x+\dfrac{\pi }{6})$              
D．$\cos (\dfrac{5\pi }{6}-2x)$
分析：根据图象先求出函数的周期，和$\omega$，利用五点法求出函数的$\varphi$的值，结合三角函数的诱导公式进行转化求解即可．
解答：由图象知函数的周期$T=2\times (\dfrac{2\pi }{3}-\dfrac{\pi }{6})=\pi$，即$\dfrac{2\pi }{\vert \omega \vert }=\pi$，即$\omega =\pm 2$，
当$\omega =2$时，由五点作图法，得$2\times \dfrac{\pi }{6}+\varphi =\pi$，所以$\varphi =\dfrac{2\pi }{3}$，
则$f(x)=\sin (2x+\dfrac{2\pi }{3})=\cos (\dfrac{\pi }{2}-2x-\dfrac{2\pi }{3})$
$=\cos (-2x-\dfrac{\pi }{6})=\cos (2x+\dfrac{\pi }{6})$
$=\sin (\dfrac{\pi }{2}-2x-\dfrac{\pi }{6})=\sin (\dfrac{\pi }{3}-2x)$，
当$\omega =-2$时，由五点作图法，得$-2\times \dfrac{\pi }{6}+\varphi =0$，所以$\varphi =\dfrac{\pi }{3}$，
所以$f(x)=\sin (-2x+\dfrac{\pi }{3})$．
故选：BC．
点评：本题主要考查三角函数解析式的求解，结合函数图象求出函数的周期和$\omega$，利用三角函数的诱导公式进行转化是解决本题的关键．比较基础．