| 2020年高考数学新高考Ⅱ-8 |
|
2021-06-08 21:52:39 |
|
|
若定义在$R$的奇函数$f(x)$在$(-\infty ,0)$单调递减,且$f(2)=0$,则满足$xf(x-1)\geqslant 0$的$x$的取值范围是( )
A.$[-1$,$1]\cup{[}3$,$+\infty )$
B.$[-3$,$-1]\cup{[}0$,$1]$
C.$[-1$,$0]\cup{[}1$,$+\infty )$
D.$[-1$,$0]\cup{[}1$,$3]$
分析:根据函数奇偶性的性质,然后判断函数的单调性,利用分类讨论思想进行求解即可.
解答:$\because$定义在$R$的奇函数$f(x)$在$(-\infty ,0)$单调递减,且$f(2)=0$,$f(x)$的大致图象如图:
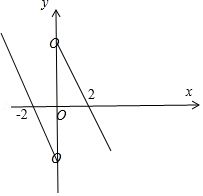
$\therefore f(x)$在$(0,+\infty )$上单调递减,且$f(-2)=0$;
故$f(-1)<0$;
当$x=0$时,不等式$xf(x-1)\geqslant 0$成立,
当$x=1$时,不等式$xf(x-1)\geqslant 0$成立,
当$x-1=2$或$x-1=-2$时,即$x=3$或$x=-1$时,不等式$xf(x-1)\geqslant 0$成立,
当$x>0$时,不等式$xf(x-1)\geqslant 0$等价为$f(x-1)\geqslant 0$,
此时$\left\{\begin{array}{l}{x>0}\\ {0<x-1\leqslant 2}\end{array}\right.$,此时$1<x\leqslant 3$,
当$x<0$时,不等式$xf(x-1)\geqslant 0$等价为$f(x-1)\leqslant 0$,
即$\left\{\begin{array}{l}{x<0}\\ {-2\leqslant x-1<0}\end{array}\right.$,得$-1\leqslant x<0$,
综上$-1\leqslant x\leqslant 0$或$1\leqslant x\leqslant 3$,
即实数$x$的取值范围是$[-1,0]\cup[1,3]$,
故选:D.
点评:本题主要考查不等式的求解,结合函数奇偶性的性质,作出函数$f(x)$的草图,是解决本题的关键.难度中等.
|
|
http://x.91apu.com//shuxue/gkt/2020/2020xgk2/2021-06-08/33120.html |

