日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为$O)$，地球上一点$A$的纬度是指$OA$与地球赤道所在平面所成角，点$A$处的水平面是指过点$A$且与$OA$垂直的平面．在点$A$处放置一个日晷，若晷面与赤道所在平面平行，点$A$处的纬度为北纬$40^\circ$，则晷针与点$A$处的水平面所成角为(　　)

A．$20^\circ$
B．$40^\circ$
C．$50^\circ$
D．$90^\circ$
分析：由纬度的定义和线面角的定义，结合直角三角形的性质，可得晷针与点$A$处的水平面所成角．
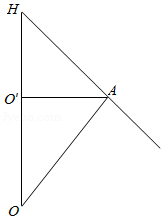
解答：可设$A$所在的纬线圈的圆心为$O'$，$OO'$垂直于纬线所在的圆面，
由图可得$\angle OHA$为晷针与点$A$处的水平面所成角，
又$\angle OAO'$为$40^\circ$且$OA\bot AH$，
在$\rm{Rt}\Delta OHA$中，$O'A\bot OH$，$\therefore \angle OHA=\angle OAO'=40^\circ$，
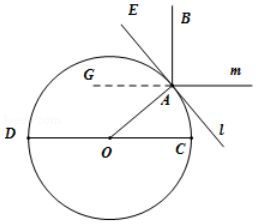
另解：画出截面图，如下图所示，其中$CD$是赤道所在平面的截线．
$l$是点$A$处的水平面的截线，由题意可得$OA\bot l$，$AB$是晷针所在直线．$m$是晷面的截线，由题意晷面和赤道面平行，晷针与晷面垂直，
根据平面平行的性质定理可得$m//CD$，
根据线面垂直的定义可得$AB\bot m$，由于$\angle AOC=40^\circ$，$m//CD$，
所以$\angle OAG=\angle AOC=40^\circ$，由于$\angle OAG+\angle GAE=\angle BAE+\angle GAE=90^\circ$，
所以$\angle BAE=\angle OAG=40^\circ$，也即晷针与$A$处的水平面所成角为$\angle BAE=40^\circ$，
故选：$B$．



点评：本题是立体几何在生活中的运用，考查空间线面角的定义和求法，属于基础题．