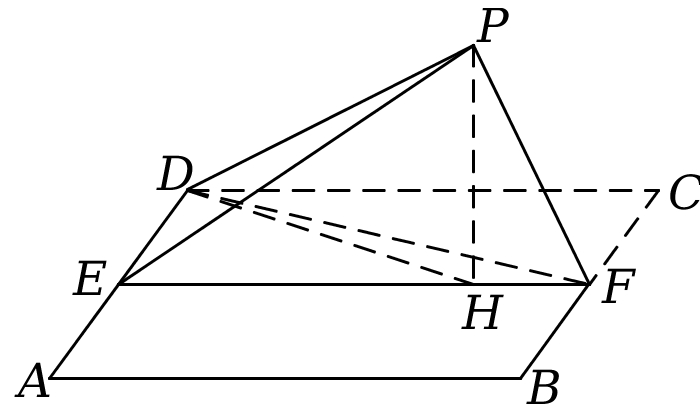
（1）证明：由题意，点$E$、$F$分别是$AD$、$BC$的中点，

则$AE=\dfrac{1}{2}AD$，$BF=\dfrac{1}{2}BC$，

由于四边形$ABCD$为正方形，所以$EF \perp BC$。

由于$PF \perp BF$，$EF \cap PF=F$，则$BF \perp 平面PEF$。

又因为$BF \subset 平面ABFD$，所以$平面PEF \perp 平面ABFD$。

（2）在$平面DEF$中，过$P$作$PH \perp EF$于点$H$，连接$DH$。

由于$EF$为面$ABCD$和面$PEF$的交线，$PH \perp EF$，

则$PH \perp 面ABFD$，故$PH \perp DH$。

在三棱锥$P-DEF$中，可以利用等体积法求$PH$。

因为$DE // BF$且$PF \perp BF$，

所以$PF \perp DE$。

又因为$\triangle PDF \cong \triangle CDF$，

所以$\angle FPD =\angle FCD =90^\circ$，

所以$PF \perp PD$。

由于$DE \cap PD =D$，则$PF\perp 平面PDE$，

故$V_{F-PDE}=\dfrac{1}{3} PF \cdot S_{\triangle PDE}$。

因为$BF // DA$且$BF \perp 面PEF$，

所以$DA \perp 面PEF$

所以$DE \perp EP$。

设正方形边长为$2a$，则$PD=2a$，$DE=a$，

在$\triangle PDE$中，$PE=\sqrt{3}a$，

所以$S_{\triangle PDE}=\dfrac{\sqrt{3}}{2}a^2$，

$V_{F-PDE}=\dfrac{\sqrt{3}}{6}a^3$。

又因为$S_{\triangle DEF}=\dfrac{1}{2} a \cdot 2a=a^2$，

所以$PH=\dfrac{3V_{F-PDE}}{a^2}=\dfrac{\sqrt{3}}{2}a$，

所以在$\triangle PHD$中，$\sin \angle PDH =\dfrac{PH}{PD}=\dfrac{\sqrt{3}}{4}$，

即$\angle PDH$为$DP$与面$ABFD$的夹角的正弦值为$\dfrac{\sqrt{3}}{4}$。