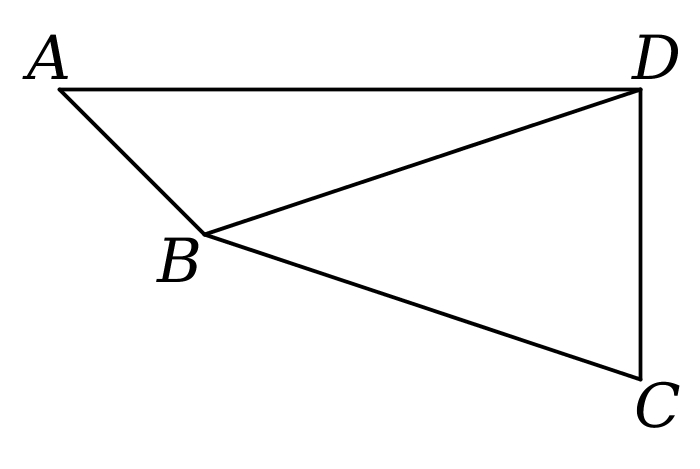
（1）如图，在$\triangle ABD$中，$AB=2$，$BD=5$，$\angle A=45^\circ$。

由正弦定理，$\dfrac{BD}{\sin 45^\circ}=\dfrac{AB}{\sin \angle ADB}$，

即$\dfrac{5}{\frac{\sqrt{2}}{2}}=\dfrac{2}{\sin \angle ADB}$，

所以$\sin \angle ADB=\dfrac{\sqrt{2}}{5}$。

因为$\angle ADC=90^\circ$，所以$\angle ADB <90^\circ$，

因为$\cos^2 \angle ADB + \sin^2 \angle ADB =1$，

所以$\cos \angle ADB=\dfrac{\sqrt{23}}{5}$。

（2）因为$CD=2\sqrt{2}$，$\angle CDB=90^\circ-\angle ADB$，

$\cos \angle CDB=\sin \angle ADB=\dfrac{\sqrt{2}}{5}$，

在$\triangle CBD$中，由余弦定理得，

$BC^2=CD^2+BD^2-2 \times CD \times BD \times \cos \angle CDB$

$=(2\sqrt{2})^2+5^2-2 \times 2\sqrt{2} \times 5 \times \dfrac{\sqrt{2}}{5}$

$=25$。

所以$BC=5$。