本题主要考查直线与圆锥曲线。

由题意$a^2=3$，$b^2=1$，

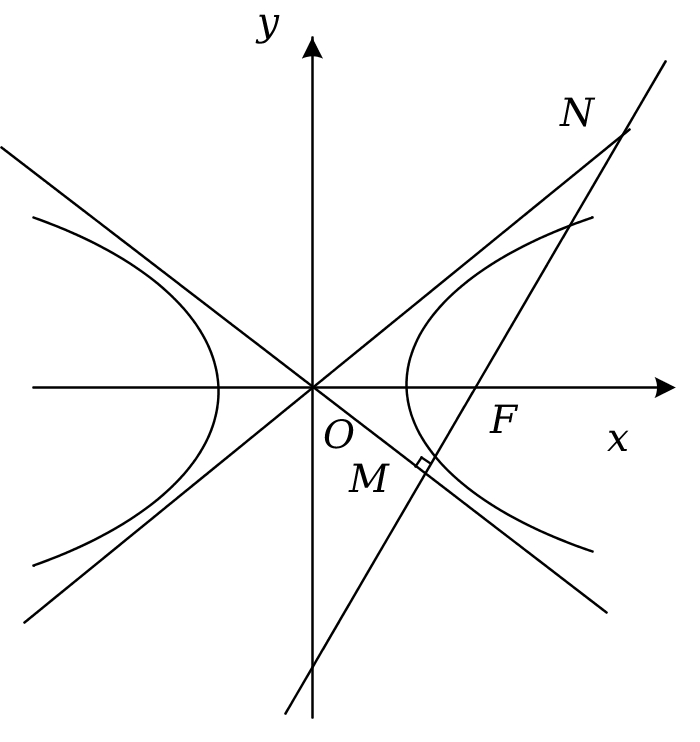
则$F(2,0)$，

$C$的渐近线方程为$y=\pm \dfrac{1}{\sqrt{3}}x$即$y=\pm \dfrac{\sqrt{3}}{3}x$，

由于$\angle NOF =\angle OMF =30^\circ$，

则$\angle NOM =60^\circ \ne 90^\circ$，

由双曲线对称性，设$\angle OMN=90^\circ$，

则$|MN|=\sqrt{3}|OM|$，

而$\angle FOM=30^\circ$，$\angle OMF=90^\circ$，$OF=2$，

则$OM=OF \cdot \cos 30^\circ =2 \times \dfrac{\sqrt{3}}{2}=\sqrt{3}$，

故$|MN|=\sqrt{3} \times \sqrt{3}=3$。

故本题正确答案为B。