本题主要考查圆锥曲线和平面向量的数量积。

过点$(-2,0)$且斜率为$\dfrac{2}{3}$的直线为$y=\dfrac{2}{3}(x+2)$①。

将直线①代入抛物线方程得$y^2=6y-8$。

解得$\begin{cases}y=2\\x=1\end{cases}$或$\begin{cases}y=4\\x=4\end{cases}$，

则$M(1,2)$，$N(4,4)$。

因为$F$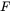为抛物线焦点，则$F(1,0)$。所以$\overrightarrow{FM}=(0,2)$，$\overrightarrow{FN}=(3,4)$。

所以$\overrightarrow{FM}\cdot\overrightarrow{FN}=0\times 3 +2 \times 4=8$。

故本题正确答案为D。