|
空间向量的概念
①向量定义:一般地,既有大小,又有方向的量叫做向量。
②相关概念:
Ⅰ、向量的模: 向量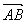 (或 (或 )的大小,就是向量 )的大小,就是向量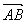 (或 (或 )的长度,称为向量的模,记作| )的长度,称为向量的模,记作|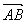 |(或 |(或 )。 )。
向量与向量的模的概念表明,向量不能比大小,向量的模可以比较大小。
Ⅱ、零向量与单位向量:
长度为0的向量叫零向量,记作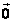 。规定零向量的方向是任意的。 。规定零向量的方向是任意的。
长度为1个单位长度的向量,叫单位向量,记作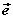 。 。
概念表明,零向量、单位向量的定义都只是限制了大小,而没确定的方向。
Ⅲ、相等向量、平行向量和共线向量:
⑴相等向量:长度相等且方向相同的向量叫做相等向量。
⑵平行向量:方向相同或相反的非零向量叫做平行向量。向量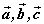 平行,记作 平行,记作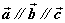 。 。
规定零向量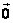 与任一向量平行,即 与任一向量平行,即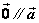 。 。
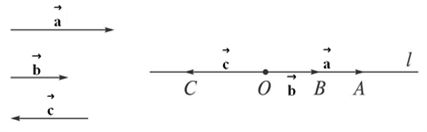
⑶共线向量:平行向量也叫做共线向量。因此,共线向量就是平行向量,平行向量就是共线向量。
⑷区别与联系:相等向量一定是平行向量,也一定是共线向量;反之,平行向量、共线向量不一定是相等向量。平行向量可以在同一条直线上,共线向量可以不在同一条直线上。
|

